��Ŀ����
����Ŀ��ij���ʳ������ס������ֻ�Ϸ��ϣ���ҪA��B��C������Ҫԭ��.����1��Ƥ���ַ��Ϻ�����1��Ƥ���ַ�����������ԭ�ϵĶ������±���ʾ��

����A��ԭ��200�֣�B��ԭ��360�֣�C��ԭ��300��.�ڴ˻����������ס������ַ���.��֪����1��Ƥ���ַ��ϣ�����������Ϊ2��Ԫ������1��Ƥ���ַ��ϣ�����������Ϊ3��Ԫ.�ֱ���x��y��ʾ�ƻ������ס������ַ��ϵij�Ƥ��.
(1)��x��y�г�����������������ѧ��ϵʽ����������Ӧ��ƽ������
(2)�ʷֱ������ס������ַ��ϸ����ٳ�Ƥ���ܹ�������������������������.
���𰸡���1�������������2���������ַ��� ![]() ��Ƥ�����ַ���
��Ƥ�����ַ��� ![]() ��Ƥʱ����������������Ϊ
��Ƥʱ����������������Ϊ ![]() ��Ԫ.
��Ԫ.
��������
�����������������������ʽ��ϵ����������������
���������Ŀ�꺯��������ƽ��ֱ�߷�������⼴�ɣ�
��1�� ����֪��![]() ��
��![]() �������ѧ��ϵʽΪ
�������ѧ��ϵʽΪ 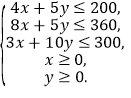
�ö�Ԫһ�β���ʽ������ʾ��ƽ������Ϊͼ1�е���Ӱ���֣�
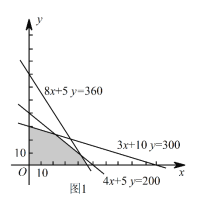
��2�� ������Ϊ ![]() ��Ԫ����Ŀ�꺯��Ϊ
��Ԫ����Ŀ�꺯��Ϊ ![]() ��
��
���� ![]() ����������Ϊ
����������Ϊ ![]() ������б��Ϊ
������б��Ϊ ![]() ����
���� ![]() �仯��һ��ƽ��ֱ�ߣ�
�仯��һ��ƽ��ֱ�ߣ� ![]() Ϊֱ����
Ϊֱ���� ![]() ���ϵĽؾ࣬��
���ϵĽؾ࣬�� ![]() ȡ���ֵʱ��
ȡ���ֵʱ��![]() ��ֵ�������Ϊ
��ֵ�������Ϊ ![]() ��
��![]() ����Լ��������������ͼ2��֪����ֱ��
����Լ��������������ͼ2��֪����ֱ�� ![]() �����������ϵĵ�
�����������ϵĵ� ![]() ʱ���ؾ�
ʱ���ؾ� ![]() ���
��� ![]() ���
���
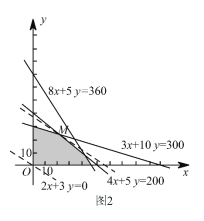
�ⷽ���� ![]() �õ�
�õ� ![]() ������Ϊ
������Ϊ ![]() ��
��
���� ![]() ��
��
���������ַ��� ![]() ��Ƥ�����ַ���
��Ƥ�����ַ��� ![]() ��Ƥʱ����������������Ϊ
��Ƥʱ����������������Ϊ ![]() ��Ԫ��
��Ԫ��

����Ŀ��ijУ�ڸ߶��꼶ʵ��ѡ���߰��ѧ��ѧУΪѧ���ṩ�˶��ֿγ̣�������ѧ���ṩ5�ֲ�ͬ��εĿγ̣��ֱ��Ϊ��ѧ1����ѧ2����ѧ3����ѧ4����ѧ5��ÿ��ѧ��ֻ�ܴ���5����ѧ�γ���ѡ��һ��ѧϰ����У�߶��꼶1800��ѧ������ѧѡ������ͳ�������
�γ� | ��ѧ1 | ��ѧ2 | ��ѧ3 | ��ѧ4 | ��ѧ5 | �ϼ� |
ѡ������ | 180 | 540 | 540 | 360 | 180 | 1800 |
Ϊ���˽���ѧ�ɼ���ѧ��ѡ�����֮��Ĺ�ϵ���÷ֲ�����ķ�������1800��ѧ���г�ȡ��10�˽��з�����
��1����ѡ����10��ѧ���������ȡ3�ˣ�����3����������2��ѡ����ѧ2�ĸ��ʣ�
��2����ѡ����10��ѧ���������ȡ3�ˣ�����3����ѡ����ѧ2������ΪX��ѡ����ѧ1������ΪY�������������=X��Y������������εķֲ��к���ѧ����E���Σ���