题目内容
设函数 ,
, .
.
(1)记 为
为 的导函数,若不等式
的导函数,若不等式 在
在 上有解,求实数
上有解,求实数 的取值范围;
的取值范围;
(2)若 ,对任意的
,对任意的 ,不等式
,不等式 恒成立,求m(m∈Z,m
恒成立,求m(m∈Z,m 1)的值.
1)的值.
(1)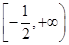 ;(2)
;(2)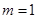 .
.
解析试题分析:(1)首先由已知条件将不等式转化为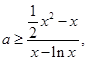 它在
它在 上有解等价于
上有解等价于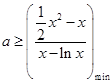 ,再利用导数求函数
,再利用导数求函数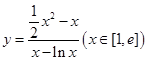 的最小值;(2)由已知
的最小值;(2)由已知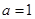 时,对任意的
时,对任意的 ,不等式
,不等式 恒成立,等价变形为
恒成立,等价变形为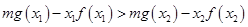 在
在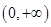 上恒成立,为此只需构造函数
上恒成立,为此只需构造函数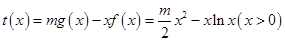 ,只要证明函数
,只要证明函数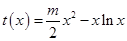 在
在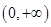 上单调递增即可.
上单调递增即可.
试题解析:(1)不等式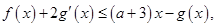 即为
即为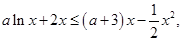 化简得
化简得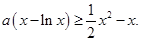 由
由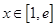 知
知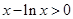 ,因而
,因而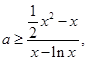 设
设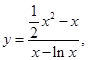 由
由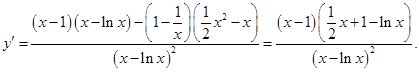
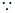 当
当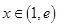 时
时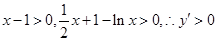 在
在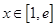 上恒成立.
上恒成立.
由不等式有解,可得知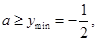 即实数
即实数 的取值范围是
的取值范围是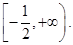
(2)当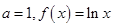 .由
.由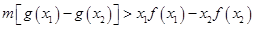 恒成立,得
恒成立,得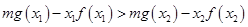 恒成立. 设
恒成立. 设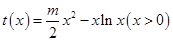 ,
,
由题意知 ,故当
,故当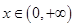 时函数
时函数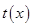 单调递增,
单调递增,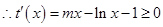 恒成立,即
恒成立,即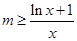 恒成立,因此,记
恒成立,因此,记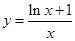 ,得
,得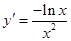 ,
,
∵函数在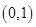 上单调递增,在
上单调递增,在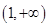 上单调递减,∴函数
上单调递减,∴函数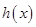 在
在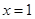 时取得极大值,并且这个极大值就是函数
时取得极大值,并且这个极大值就是函数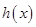 的最大值.由此可得
的最大值.由此可得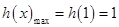 ,故
,故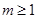 ,结合已知条件
,结合已知条件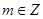 ,
,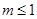 ,可得
,可得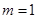 .
.
考点:1.导数的应用;2.恒成立问题中的参数取值范围问题.

练习册系列答案
 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目
 .
. 的极大值和极小值;
的极大值和极小值; 时,
时, 恒成立,求
恒成立,求 的取值范围.
的取值范围. .
. 时,求曲线
时,求曲线 在
在 处的切线方程;
处的切线方程; 的单调性.
的单调性.
 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程; 的单调区间;
的单调区间; 的取值范围.
的取值范围. ,函数
,函数 .
. 时,写出函数
时,写出函数 的单调递增区间;
的单调递增区间; 时,求函数
时,求函数 ,函数
,函数 ,其中
,其中 是自然对数的底数.
是自然对数的底数. 的单调区间和极值;
的单调区间和极值; 对任意
对任意 满足
满足 ,求证:当
,求证:当 时,
时, ;
; ,且
,且 ,求证:
,求证: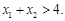
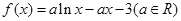 。
。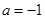 ,求函数
,求函数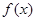 的单调区间并比较
的单调区间并比较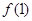 的大小关系
的大小关系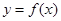 的图象在点
的图象在点 处的切线的倾斜角为
处的切线的倾斜角为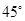 ,对于任意的
,对于任意的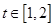 ,函数
,函数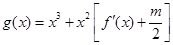 在区间
在区间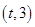 上总不是单调函数,求
上总不是单调函数,求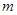 的取值范围;
的取值范围;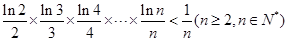 。
。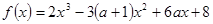 ,其中
,其中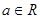 .
.  在
在 处取得极值,求常数
处取得极值,求常数 的值;
的值; ,
, ,若
,若 元素中有唯一的整数,求
元素中有唯一的整数,求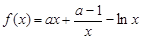
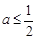 时,试讨论函数
时,试讨论函数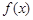 的单调性;
的单调性;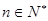 ,有
,有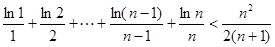 .
.