题目内容
已知 ,函数
,函数 .
.
(1)当 时,写出函数
时,写出函数 的单调递增区间;
的单调递增区间;
(2)当 时,求函数
时,求函数 在区间[1,2]上的最小值;
在区间[1,2]上的最小值;
(3)设 ,函数
,函数 在(m,n)上既有最大值又有最小值,请分别求出m,n的取值范围(用a表示).
在(m,n)上既有最大值又有最小值,请分别求出m,n的取值范围(用a表示).
(1)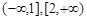 ;(2)
;(2)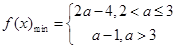 ;(3)详见解析.
;(3)详见解析.
解析试题分析:(1)对于含绝对值的函数一般可通过讨论去掉绝对值化为分段函数再解答,本题当 时,函数去掉绝对值后可发现它的图象是由两段抛物线的各自一部分组成,画出其图象,容易判断函数
时,函数去掉绝对值后可发现它的图象是由两段抛物线的各自一部分组成,画出其图象,容易判断函数 的单调递增区间;(2)
的单调递增区间;(2)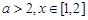 时,所以
时,所以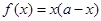 ,这是二次函数,求其在闭区间上
,这是二次函数,求其在闭区间上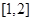 的最小值,一般要分类讨论,考虑对称轴和区间的相对位置关系,从而判断其单调性,从而求出最小值;(3)函数在开区间上有最大值和最小值,必然要使开区间上有极大值和极小值,且使极值为最值,由于函数是与二次函数相关,可考虑用数形结合的方法解答.
的最小值,一般要分类讨论,考虑对称轴和区间的相对位置关系,从而判断其单调性,从而求出最小值;(3)函数在开区间上有最大值和最小值,必然要使开区间上有极大值和极小值,且使极值为最值,由于函数是与二次函数相关,可考虑用数形结合的方法解答.
试题解析:(1)当 时,
时,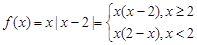 , 2分
, 2分
由图象可知,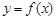 的单调递增区间为
的单调递增区间为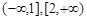 . 4分
. 4分
(2)因为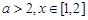 ,所以
,所以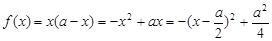 . 6分
. 6分
当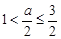 ,即
,即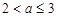 时,
时,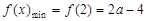 ; 7分
; 7分
当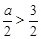 ,即
,即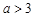 时,
时,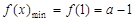 . 8分
. 8分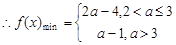 . 9分
. 9分
(3)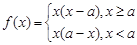 , 10分
, 10分
①当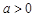 时,图象如图1所示.
时,图象如图1所示.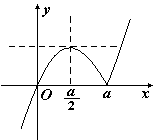
图1
由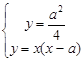 得
得 . 12分
. 12分
②当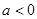 时,图象如图2所示.
时,图象如图2所示.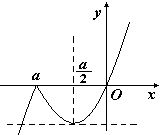
图2
由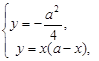 得
得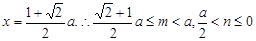 . 14分
. 14分
考点:含绝对值的函数、二次函数.

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
 ,其中
,其中 .
. 时判断
时判断 的单调性;
的单调性; 在其定义域为增函数,求正实数
在其定义域为增函数,求正实数 的取值范围;
的取值范围; ,当
,当 时,若
时,若 ,总有
,总有 成立,求实数
成立,求实数 的取值范围.
的取值范围.
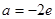 时,求函数
时,求函数 的单调区间和极值;
的单调区间和极值; 在[1,4]上是减函数,求实数
在[1,4]上是减函数,求实数 的取值范围.
的取值范围. ,曲线
,曲线 过点
过点 ,且在
,且在 点处的切线斜率为2.
点处的切线斜率为2. .
. 为函数
为函数 图象上一点,
图象上一点, 为坐标原点,记直线
为坐标原点,记直线 的斜率
的斜率 .
. 在区间
在区间 上存在极值,求实数
上存在极值,求实数 的取值范围;
的取值范围; 时,不等式
时,不等式 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
 ,
, .
. 为
为 的导函数,若不等式
的导函数,若不等式 在
在 上有解,求实数
上有解,求实数 的取值范围;
的取值范围; ,对任意的
,对任意的 ,不等式
,不等式 恒成立,求m(m∈Z,m
恒成立,求m(m∈Z,m 1)的值.
1)的值. .
. 的单调区间;
的单调区间; ,若
,若 在
在 上单调递增,求
上单调递增,求 的取值范围.
的取值范围. (其中
(其中 ),且方程
),且方程 的两个根分别为
的两个根分别为 、
、 .
. 且曲线
且曲线 过原点时,求
过原点时,求 的解析式;
的解析式; 无极值点,求
无极值点,求 的取值范围.
的取值范围.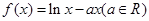
 的单调区间;
的单调区间; 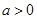 时,求函数
时,求函数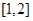 上的最小值.
上的最小值.