题目内容
已知向量
=(cos(-θ),sin(-θ)),
=(cos(
-θ),sin(
-θ)),设
=
+(x2+3)
,
=-y
+x
,且满足
⊥
.
(1)写出y关于x的函数关系式y=f(x);
(2)设函数g(x)=f(x)-ax在(-1,1)上单调递减,求a的取值范围.
| a |
| b |
| π |
| 2 |
| π |
| 2 |
| m |
| a |
| b |
| n |
| a |
| b |
| m |
| n |
(1)写出y关于x的函数关系式y=f(x);
(2)设函数g(x)=f(x)-ax在(-1,1)上单调递减,求a的取值范围.
考点:平面向量数量积的运算
专题:平面向量及应用
分析:(1)先根据已知条件求出
,
,而
⊥
,所以有
•
=0,要求
•
先求出
2=
2=1,
•
=0,这样即可得到
•
,从而得到y=x3+3x;
(2)先求g(x)=x3+(3-a)x,g′(x)=3x2+3-a,根据已知条件知3x2+3-a≤0在(-1,1)上恒成立.所以a≥3x2+3在(-1,1)上恒成立,因为x∈(-1,1)时,3x2+3<6,所以得出a≥6.
| a |
| b |
| m |
| n |
| m |
| n |
| m |
| n |
| a |
| b |
| a |
| b |
| m |
| n |
(2)先求g(x)=x3+(3-a)x,g′(x)=3x2+3-a,根据已知条件知3x2+3-a≤0在(-1,1)上恒成立.所以a≥3x2+3在(-1,1)上恒成立,因为x∈(-1,1)时,3x2+3<6,所以得出a≥6.
解答:
解:(1)由已知
=(cosθ,-sinθ),
=(sinθ,cosθ);
∴|
|=|
|=1;
∴
•
=cosθsinθ-sinθcosθ=0;
∵
⊥
;
∴
•
=[
+(x2+3)
]•[-y
+x
]=-y
2+x(x2+3)
2+[x-y(x2+3)]
•
=-y+x(x2+3)=0;
∴y=x3+3x;
即f(x)=x3+3x;
(2)g(x)=f(x)-ax=x3+(3-a)x;
g′(x)=3x2+3-a;
∵函数g(x)在(-1,1)上单调递减;
∴g′(x)≤0在(-1,1)上恒成立,即:
3x2+3-a≤0,a≥3x2+3在x∈(-1,1)上恒成立;
∵x∈(-1,1)时,3x2+3<6;
∴a≥6;
∴a的取值范围为[6,+∞).
| a |
| b |
∴|
| a |
| b |
∴
| a |
| b |
∵
| m |
| n |
∴
| m |
| n |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
∴y=x3+3x;
即f(x)=x3+3x;
(2)g(x)=f(x)-ax=x3+(3-a)x;
g′(x)=3x2+3-a;
∵函数g(x)在(-1,1)上单调递减;
∴g′(x)≤0在(-1,1)上恒成立,即:
3x2+3-a≤0,a≥3x2+3在x∈(-1,1)上恒成立;
∵x∈(-1,1)时,3x2+3<6;
∴a≥6;
∴a的取值范围为[6,+∞).
点评:考查根据向量坐标求向量长度,向量数量积的坐标运算,以及非零向量垂直的充要条件,函数单调性和函数导数符号的关系.

练习册系列答案
相关题目
设a>0,b>0且a+b=1则
+
的最小值是( )
| 1 |
| a |
| 2 |
| b |
| A、2 | ||
| B、4 | ||
C、3+2
| ||
| D、6 |
| 1 |
| 2 |
| A、2+2i | B、2-2i |
| C、i | D、-i |
tan
π的值为( )
| 16 |
| 3 |
A、-
| ||||
B、
| ||||
C、
|
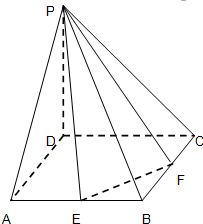 已知正方形ABCD,边长为1,过D作PD⊥平面ABCD,且PD=2,E,F分别是AB和BC的中点.
已知正方形ABCD,边长为1,过D作PD⊥平面ABCD,且PD=2,E,F分别是AB和BC的中点.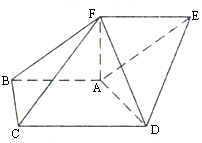 在五面体ABCDEF中,AB∥DC,∠BAD=
在五面体ABCDEF中,AB∥DC,∠BAD=