题目内容
半径为1的球面上有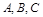 三点,其中点
三点,其中点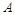 与
与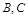 两点间的球面距离均为
两点间的球面距离均为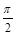 ,
,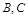 两点间的球面距离为
两点间的球面距离为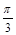 ,则球心到平面
,则球心到平面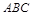 的距离为( )
的距离为( )
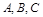 三点,其中点
三点,其中点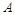 与
与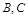 两点间的球面距离均为
两点间的球面距离均为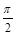 ,
,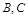 两点间的球面距离为
两点间的球面距离为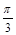 ,则球心到平面
,则球心到平面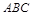 的距离为( )
的距离为( )A. | B. | C. | D. |
B
试题分析:根据题意可知:球心O与A,B,C三点构成三棱锥O-ABC,且OA=OB=OC=R=1,∠AOB=∠AOC=90°,∠BOC=60°,故AO⊥面BOC.所以此题可以根据体积法求得球心O到平面ABC的距离. 解:球心O与A,B,C三点构成三棱锥O-ABC,如图所示,
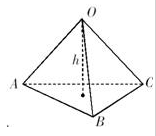
已知OA=OB=OC=R=1,∠AOB=∠AOC=90°,∠BOC=60°,由此可得AO⊥面BOC.∵S△BOC=
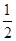 ,S△ABC=
,S△ABC=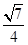 .
.∴由VA-BOC=VO-ABC,得 h=
 .故选B.
.故选B.点评:本小题主要考查立体几何球面距离及点到面的距离、三棱锥的结构等基础知识,考查运算求解能力,考查空间想象力.属于基础题

练习册系列答案
相关题目
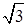 ,AD=CD=1.
,AD=CD=1.
 求证:BD⊥AA1;
求证:BD⊥AA1; 若四边形
若四边形 是菱形,且
是菱形,且 ,求四棱柱
,求四棱柱 的体积.
的体积. ,那么正方体的棱长等于________。
,那么正方体的棱长等于________。
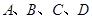 在同一个球的球面,
在同一个球的球面,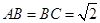 ,
,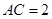 ,若四面体
,若四面体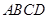 体积的最大值为
体积的最大值为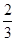 ,则这个球的表面积为( )
,则这个球的表面积为( )



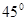 ,容器的高为10cm,制作该容器需要 cm2的铁皮
,容器的高为10cm,制作该容器需要 cm2的铁皮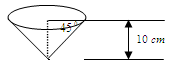



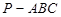 的外接球的球心
的外接球的球心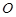 在
在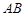 上,且
上,且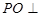 平面
平面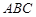 ,
, 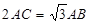 , 若四面体
, 若四面体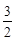 ,则该球的体积为___________;
,则该球的体积为___________;