题目内容
(本题满分12分) 如图,正三棱柱ABC—A1B1C1的所有棱长均为2,P是侧棱AA1上任意一点.

(1)求证:B1P不可能与平面ACC1A1垂直;
(2)当BC1⊥B1P时,求线段AP的长;
(3)在(2)的条件下,求二面角CB1PC1的大小.

(1)求证:B1P不可能与平面ACC1A1垂直;
(2)当BC1⊥B1P时,求线段AP的长;
(3)在(2)的条件下,求二面角CB1PC1的大小.
(2) AP="1 " (3) arctan

(1)证明:连结B1P,假设B1P⊥平面ACC1A1,

则B1P⊥A1C1. 由于三棱柱ABC—A1B1C1为正三棱柱,
∴AA1⊥A1C1. ∴A1C1⊥侧面ABB1A1. ∴A1C1⊥A1B1, 即∠B1A1C1=90°.
这与△A1B1C1是等边三角形矛盾. ∴B1P不可能与平面ACC1A1垂直.
(2)取A1B1的中点D,连结C1D、BD、BC1, 则C1D⊥A1B1, 又∵AA1⊥平面A1B1C1,
∴AA1⊥C1D. ∴C1D⊥平面ABB1A1. ∴BD是BC1在平面ABB1A1上的射影.
∵BC1⊥B1P. ∴BD⊥B1P. ∴∠B1BD=90°-∠BB1P=∠A1B1P. 又A1B1=B1B=2,
∴△BB1D≌△B1A1P,A1P=B1D="1. " ∴AP=1.
(3)连结B1C,交BC1于点O,则BC1⊥B1C. 又BC1⊥B1P, ∴BC1⊥平面B1CP. 过O在平面CPB1上作OE⊥B1P,交B1P于点E,连结C1E,则B1P⊥C1E, ∴∠OEC1是二面角C-B1P-C1的平面角.
由于CP=B1P= ,O为B1C的中点,连结OP, ∴PO⊥B1C,OP·OB1=OE·B1P.∴OE=
,O为B1C的中点,连结OP, ∴PO⊥B1C,OP·OB1=OE·B1P.∴OE= .
.
∴tan∠OEC1= =
= .∴∠OEC1=arctan
.∴∠OEC1=arctan . 故二面角CB1PC1的大小为arctan
. 故二面角CB1PC1的大小为arctan .
.

则B1P⊥A1C1. 由于三棱柱ABC—A1B1C1为正三棱柱,
∴AA1⊥A1C1. ∴A1C1⊥侧面ABB1A1. ∴A1C1⊥A1B1, 即∠B1A1C1=90°.
这与△A1B1C1是等边三角形矛盾. ∴B1P不可能与平面ACC1A1垂直.
(2)取A1B1的中点D,连结C1D、BD、BC1, 则C1D⊥A1B1, 又∵AA1⊥平面A1B1C1,
∴AA1⊥C1D. ∴C1D⊥平面ABB1A1. ∴BD是BC1在平面ABB1A1上的射影.
∵BC1⊥B1P. ∴BD⊥B1P. ∴∠B1BD=90°-∠BB1P=∠A1B1P. 又A1B1=B1B=2,
∴△BB1D≌△B1A1P,A1P=B1D="1. " ∴AP=1.
(3)连结B1C,交BC1于点O,则BC1⊥B1C. 又BC1⊥B1P, ∴BC1⊥平面B1CP. 过O在平面CPB1上作OE⊥B1P,交B1P于点E,连结C1E,则B1P⊥C1E, ∴∠OEC1是二面角C-B1P-C1的平面角.
由于CP=B1P=
 ,O为B1C的中点,连结OP, ∴PO⊥B1C,OP·OB1=OE·B1P.∴OE=
,O为B1C的中点,连结OP, ∴PO⊥B1C,OP·OB1=OE·B1P.∴OE= .
. ∴tan∠OEC1=
 =
= .∴∠OEC1=arctan
.∴∠OEC1=arctan . 故二面角CB1PC1的大小为arctan
. 故二面角CB1PC1的大小为arctan .
.
练习册系列答案
相关题目
 ⊙O所在的平面,
⊙O所在的平面, 是⊙O的直径,
是⊙O的直径, ,
, C是⊙O上一点,且
C是⊙O上一点,且 ,
, 与⊙O所在的平面成
与⊙O所在的平面成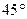 角,
角, 是
是 ;(Ⅱ) 求证:
;(Ⅱ) 求证: ;
; 倍,P为侧棱SD上的点。
倍,P为侧棱SD上的点。 
 的经线上有A、B两点,A在北纬
的经线上有A、B两点,A在北纬 ,则它们的球面距离是__________.
,则它们的球面距离是__________.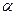 和共面的直线
和共面的直线 、
、 下列命题中真命题是
下列命题中真命题是 则
则 B.若
B.若 则
则
 则
则 与
与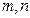 是两条不同的直线,
是两条不同的直线, 是两个不同的平面,下列命题正确的是( )
是两个不同的平面,下列命题正确的是( ) ,则
,则
 则
则
 ,则
,则
 则
则