题目内容
【题目】设函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)若函数![]() 存在两个零点
存在两个零点![]() .
.
①实数![]() 的取值范围;
的取值范围;
②证明:![]() .
.
【答案】(1)![]() ;(2)①
;(2)①![]() ;②详见解析.
;②详见解析.
【解析】
(1)求得![]() 的导数,可得切线的斜率,由点斜式方程可得切线方程;
的导数,可得切线的斜率,由点斜式方程可得切线方程;
(2)①求得![]() 的导数,讨论
的导数,讨论![]() 的符号,求得单调性,结合函数的零点,可得最小值小于
的符号,求得单调性,结合函数的零点,可得最小值小于![]() ,解不等式可得
,解不等式可得![]() 的范围;
的范围;
②由题意可得![]() ,作差可得
,作差可得![]() ,运用分析法证明,转化为证明
,运用分析法证明,转化为证明![]() ,设
,设![]() ,可得
,可得![]() ,设
,设![]() ,求得导数,判断单调性,即可得证.
,求得导数,判断单调性,即可得证.
(1)函数![]() 的导函数为
的导函数为![]() ,
,
可得![]() 在
在![]() 处切线的斜率为
处切线的斜率为![]() ,
,
则切线方程为![]() ,即
,即![]() .
.
(2)
①函数![]() 的导函数为
的导函数为![]() ,
,
若![]() ,则
,则![]() 在
在![]() 上递增,不成立;
上递增,不成立;
当![]() 时,
时,![]() 在
在![]() 时递增,在
时递增,在![]() 时递减,
时递减,
所以![]() 在
在![]() 处取得极小值,且为最小值
处取得极小值,且为最小值![]() ,
,
由题意可得![]() ,解得
,解得![]() .
.
②依题意可得![]() ,
,
两式相减并化简得![]() ,要证
,要证![]() ,
,
即证![]() ,
,
即为![]() ,即为
,即为![]() ,即为
,即为![]() ,
,
由![]() 可得
可得![]() ,设
,设![]() ,
,
可得![]() ,
,
设![]() ,
,
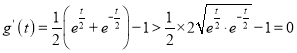 ,
,
则![]() 在
在![]() 递增,而
递增,而![]() ,所以
,所以![]() ,
,
所以![]() ,
,
则![]() .
.

 初中学业考试导与练系列答案
初中学业考试导与练系列答案【题目】推进垃圾分类处理,是落实绿色发展理念的必然选择,也是打赢污染防治攻坚战的重要环节.为了解居民对垃圾分类的了解程度,某社区居委会随机抽取1000名社区居民参与问卷测试,并将问卷得分绘制频率分布表如下:
得分 |
|
|
|
|
|
|
|
男性人数 | 40 | 90 | 120 | 130 | 110 | 60 | 30 |
女性人数 | 20 | 50 | 80 | 110 | 100 | 40 | 20 |
(1)从该社区随机抽取一名居民参与问卷测试,试估计其得分不低于60分的概率;
(2)将居民对垃圾分类的了解程度分为“比较了解“(得分不低于60分)和“不太了解”(得分低于60分)两类,完成![]() 列联表,并判断是否有95%的把握认为“居民对垃圾分类的了解程度”与“性别”有关?
列联表,并判断是否有95%的把握认为“居民对垃圾分类的了解程度”与“性别”有关?
不太了解 | 比较了解 | |
男性 | ||
女性 |
(3)从参与问卷测试且得分不低于80分的居民中,按照性别进行分层抽样,共抽取10人,连同![]() 名男性调查员一起组成3个环保宜传队.若从这
名男性调查员一起组成3个环保宜传队.若从这![]() 中随机抽取3人作为队长,且男性队长人数占的期望不小于2.求
中随机抽取3人作为队长,且男性队长人数占的期望不小于2.求![]() 的最小值.
的最小值.
附:![]()
临界值表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |