题目内容
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系中,已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),点
为参数),点![]() 是曲线
是曲线![]() 上的一动点,以坐标原点为极点,
上的一动点,以坐标原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的方程为
的方程为![]()
![]() .
.
(Ⅰ)求线段![]() 的中点
的中点![]() 的轨迹的极坐标方程;
的轨迹的极坐标方程;
(Ⅱ)求曲线![]() 上的点到直线
上的点到直线![]() 的距离的最大值.
的距离的最大值.
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]()
【解析】试题分析:(1)由中点坐标公式得到M点坐标为![]() ,消参得到直角坐标,再化为极坐标方程;(2)写出直线的直角坐标方程,转化为圆心到直线的距离加减半径。
,消参得到直角坐标,再化为极坐标方程;(2)写出直线的直角坐标方程,转化为圆心到直线的距离加减半径。
解析:
(Ⅰ)设线段![]() 的中点
的中点![]() 的坐标为
的坐标为![]() ,
,
由中点坐标公式得![]() (
(![]() 为参数),
为参数),
消去参数得![]() 的轨迹的直角坐标方程为
的轨迹的直角坐标方程为![]() ,
,
由互化公式可得点![]() 的轨迹的极坐标方程为
的轨迹的极坐标方程为![]() .
.
(Ⅱ)由直线![]() 的极坐标方程为
的极坐标方程为![]() ,得
,得![]() ,
,
所以直线![]() 的直角坐标方程为
的直角坐标方程为![]() ,
,
曲线![]() 的普通方程为
的普通方程为![]() ,它表示以
,它表示以![]() 为圆心,2为半径的圆,
为圆心,2为半径的圆,
则圆心到直线![]() 的距离为
的距离为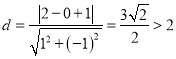 ,所以直线
,所以直线![]() 与圆相离,
与圆相离,
故曲线![]() 上的点到直线
上的点到直线![]() 的距离的最大值为
的距离的最大值为![]() .
.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目