题目内容
设f(x)是R上的奇函数, 且在(0, +∞)上递增, 若f(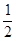 )="0," f(log4x)>0, 那么x的取值范围是( )
)="0," f(log4x)>0, 那么x的取值范围是( )
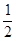 )="0," f(log4x)>0, 那么x的取值范围是( )
)="0," f(log4x)>0, 那么x的取值范围是( )A.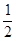 <x<1 <x<1 | B.x>2 |
C.x>2或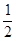 <x<1 <x<1 | D.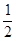 <x<1或1<x<2 <x<1或1<x<2 |
C
试题分析:因为f(x)是R上的奇函数, 且在(0, +∞)上递增, 若f(
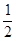 )=0,所以当
)=0,所以当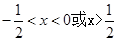 时,f(x)>0,所以由f(log4x)>0得
时,f(x)>0,所以由f(log4x)>0得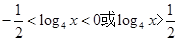 ,解得x>2或
,解得x>2或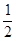 <x<1。因此选C。
<x<1。因此选C。点评:奇偶函数不等式求解时,要注意到:奇函数在关于原点对称的区间上的单调性相同,偶函数在关于原点对称的区间上的单调性相反。此题就是根据此条性质,数形结合来做的。

练习册系列答案
相关题目
 的图像关于点
的图像关于点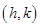 成中心对称,则函数
成中心对称,则函数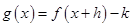 一定是( )
一定是( )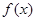 为奇函数,当
为奇函数,当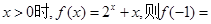 __________
__________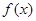
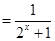
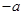 为奇函数,则
为奇函数,则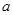 =
= 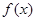 在R上的任一取值都有导数,且
在R上的任一取值都有导数,且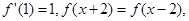 则曲线
则曲线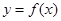 在
在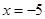 处的切线的斜率为 ( )
处的切线的斜率为 ( )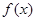 是
是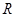 上的偶函数,且满足
上的偶函数,且满足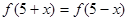 ,在[0,5]上有且只有
,在[0,5]上有且只有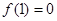 ,则
,则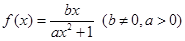 .
. 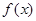 的奇偶性;
的奇偶性;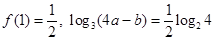 ,求
,求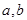 的值.
的值.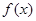 是
是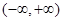 上的偶函数,
上的偶函数,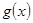 是
是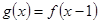 ,
,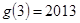 ,则
,则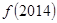 的值为_________.
的值为_________.