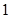题目内容
已知偶函数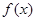 在R上的任一取值都有导数,且
在R上的任一取值都有导数,且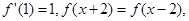 则曲线
则曲线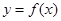 在
在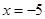 处的切线的斜率为 ( )
处的切线的斜率为 ( )
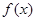 在R上的任一取值都有导数,且
在R上的任一取值都有导数,且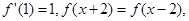 则曲线
则曲线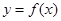 在
在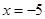 处的切线的斜率为 ( )
处的切线的斜率为 ( )| A.2 | B.-2 | C.1 | D.-1 |
D
试题分析:由f(x)在R上可导,对f(x+2)=f(x-2)两边求导得:
f′(x+2)(x+2)′=f′(x-2)(x-2)′,即f′(x+2)=f′(x-2)①,
由f(x)为偶函数,得到f(-x)=f(x),
故f′(-x)(-x)′=f′(x),即f′(-x)=-f′(x)②,
则f′(x+2+2)=f′(x+2-2),即f′(x+4)=f′(x),
所以f′(-5)=f′(-1)=-f′(1)=-1,即所求切线的斜率为-1.
故选D。
点评:中档题,本题解答充分借助于已知等式,通过两边求导数,确定得到函数导数值关系,进一步将切线斜率转化成求函数的导数值。

练习册系列答案
相关题目
 是R上的奇函数,且当
是R上的奇函数,且当 时,
时,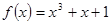 ,求
,求 ,
,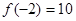 ,则
,则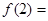 。
。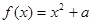 .
.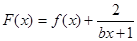 是偶函数,在定义域上
是偶函数,在定义域上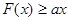 恒成立,求实数
恒成立,求实数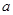 的取值范围;
的取值范围;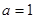 时,令
时,令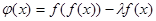 ,问是否存在实数
,问是否存在实数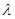 ,使
,使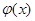 在
在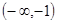 上是减函数,在
上是减函数,在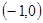 上是增函数?如果存在,求出
上是增函数?如果存在,求出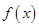 在
在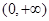 上是增函数.若
上是增函数.若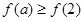 ,则实数
,则实数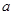 的取值范围是_________
的取值范围是_________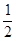 )="0," f(log4x)>0, 那么x的取值范围是( )
)="0," f(log4x)>0, 那么x的取值范围是( )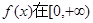 上是减函数,
上是减函数,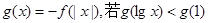 ,则x的取值
,则x的取值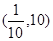
 )
)
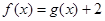 ,且
,且 为奇函数,若
为奇函数,若 ,则
,则 的值为
的值为