题目内容
【题目】已知椭圆C: ![]() =1(a>b>0)的左、右焦点为F1、F2 , 离心率为e.直线l:y=ex+a与x轴、y轴分别交于点A、B,M是直线l与椭圆C的一个公共点,P是点F1关于直线l的对称点,设
=1(a>b>0)的左、右焦点为F1、F2 , 离心率为e.直线l:y=ex+a与x轴、y轴分别交于点A、B,M是直线l与椭圆C的一个公共点,P是点F1关于直线l的对称点,设 ![]() =λ
=λ ![]() .
.
(1)证明:λ=1﹣e2;
(2)若λ= ![]() ,△MF1F2的周长为6;写出椭圆C的方程;
,△MF1F2的周长为6;写出椭圆C的方程;
(3)确定λ的值,使得△PF1F2是等腰三角形.
【答案】
(1)证明:因为A、B分别是直线l:y=ex+a与x轴、y轴的交点,
所以A、B的坐标分别是(﹣ ![]() ,0),(0,a).
,0),(0,a).
由 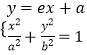 得
得  这里c=
这里c= ![]() .
.
所以点M的坐标是(﹣c, ![]() ).
).
由 ![]() =λ
=λ ![]() 得(﹣c+
得(﹣c+ ![]() ,
, ![]() )=λ(
)=λ( ![]() ,a).
,a).
即 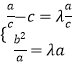 ,解得λ=1﹣e2
,解得λ=1﹣e2
(2)解:当λ= ![]() 时,e=
时,e= ![]() ,所以a=2c.
,所以a=2c.
由△PF1F2的周长为6,得2a+2c=6.
所以a=2,c=1,b2=a2﹣c2=3.
椭圆方程为 ![]() .
.
(3)解:因为PF1⊥l,所以∠PF1F2=90°+∠BAF1为钝角,要使△PF1F2为等腰三角形,必有|PF1|=|F1F2|,
即 ![]() |PF1|=c.
|PF1|=c.
设点F1到l的距离为d,由 ![]() |PF1|=d=
|PF1|=d= ![]() =
= ![]() =c.
=c.
得 ![]() =e.
=e.
所以e2= ![]() ,于是λ=1﹣e2=
,于是λ=1﹣e2= ![]() .
.
即当λ= ![]() 时,△PF1F2为等腰三角形
时,△PF1F2为等腰三角形
【解析】(1)先根据A、B分别是直线l:y=ex+a与x轴、y轴的交点表示出A、B的坐标,然后联立直线方程与椭圆方程可得到交点M的坐标,再根据 ![]() =λ
=λ ![]() 得(﹣c+
得(﹣c+ ![]() ,
, ![]() )=λ(
)=λ( ![]() ,a)根据对应坐标相等可得到
,a)根据对应坐标相等可得到 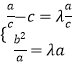 ,从而得到λ=1﹣e2 , 等证.(2)当λ=
,从而得到λ=1﹣e2 , 等证.(2)当λ= ![]() 时可得到e的值,进而得到a,c的关系,再由△PF1F2的周长为6可得到2a+2c=6,进而可求出a,c的值,从而可得到b的值,确定椭圆方程.(3)根据PF1⊥l,可得到∠PF1F2=90°+∠BAF1为钝角,进而要使得△PF1F2为等腰三角形,必有|PF1|=|F1F2|,即
时可得到e的值,进而得到a,c的关系,再由△PF1F2的周长为6可得到2a+2c=6,进而可求出a,c的值,从而可得到b的值,确定椭圆方程.(3)根据PF1⊥l,可得到∠PF1F2=90°+∠BAF1为钝角,进而要使得△PF1F2为等腰三角形,必有|PF1|=|F1F2|,即 ![]() |PF1|=c成立,然后设点F1到l的距离为d,根据
|PF1|=c成立,然后设点F1到l的距离为d,根据 ![]() |PF1|=d=
|PF1|=d= ![]() =c可得到
=c可得到 ![]() =e,进而可得到e的值,求出λ的值.
=e,进而可得到e的值,求出λ的值.
【考点精析】通过灵活运用椭圆的标准方程,掌握椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() 即可以解答此题.
即可以解答此题.

 阅读快车系列答案
阅读快车系列答案
