题目内容
【题目】已知函数f(x)=x|x﹣a|,a∈R,g(x)=x2﹣1.
(1)当a=1时,解不等式f(x)≥g(x);
(2)记函数f(x)在区间[0,2]上的最大值为F(a),求F(a)的表达式.
【答案】
(1)解:f(x)≥g(x),a=1时,即解不等式x|x﹣1|≥x2﹣1,
当x≥1时,不等式为x2﹣x≥x2﹣1,解得x≤1,所以x=1;
当x<1时,不等式为x﹣x2≥x2﹣1,解得 ![]() ,
,
所以 ![]() ;
;
综上,x∈ ![]() .
.
(2)解:因为x∈[0,2],当a≤0时,f(x)=x2﹣ax,则f(x)在区间[0,2]上是增函数,
所以F(a)=f(2)=4﹣2a;
当0<a<2时, ![]() ,
,
则f(x)在区间 ![]() 上是增函数,在区间
上是增函数,在区间 ![]() 上是减函数,在区间[a,2]上是增函数,
上是减函数,在区间[a,2]上是增函数,
所以F(a)=max{f( ![]() ),f(2)},
),f(2)},
而 ![]() ,f(2)=4﹣2a,令
,f(2)=4﹣2a,令 ![]() 即
即 ![]() ,
,
解得 ![]() ,
,
所以当 ![]() 时,F(a)=4﹣2a;
时,F(a)=4﹣2a;
令 ![]() 即
即 ![]() ,解得
,解得 ![]() 或
或 ![]() ,
,
所以当 ![]() 时,
时, ![]() ;
;
当a≥2时,f(x)=﹣x2+ax,
当 ![]() 即2≤a<4时,f(x)在间
即2≤a<4时,f(x)在间 ![]() 上是增函数,在
上是增函数,在 ![]() 上是减函数,
上是减函数,
则 ![]() ;
;
当 ![]() ,即a≥4时,f(x)在间[0,2]上是增函数,则F(a)=f(2)=2a﹣4;
,即a≥4时,f(x)在间[0,2]上是增函数,则F(a)=f(2)=2a﹣4;
所以, 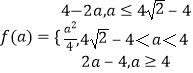
【解析】(1)当a=1时,即解不等式x|x﹣1|≥x2﹣1|,分类讨论,分别解关于x的不等式,最后取两部分的并集即可得到原不等式的解集;(2)由题意,分类讨论,确定函数的单调性,可得F(a)的表达式.

练习册系列答案
相关题目