题目内容
(10分)证明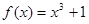 为R上的单调递增函数
为R上的单调递增函数
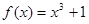 为R上的单调递增函数
为R上的单调递增函数见解析。
试题分析:设
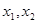 是R上的任意两个实数且
是R上的任意两个实数且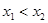 ,则
,则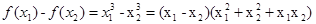 ,因为
,因为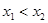 ,所以x1-x2<0.有x12+x22+x1x2>0,
,所以x1-x2<0.有x12+x22+x1x2>0,所以(x1-x 2)( x12+x22+x1x2)<0,即
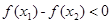 ,所以
,所以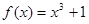 为R上的单调递增函数。
为R上的单调递增函数。点评:用定义证明函数单调性的步骤:一设二作差三变形四判断符号五得出结论。

练习册系列答案
相关题目
题目内容
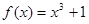 为R上的单调递增函数
为R上的单调递增函数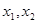 是R上的任意两个实数且
是R上的任意两个实数且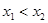 ,则
,则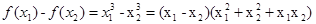 ,因为
,因为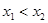 ,所以x1-x2<0.有x12+x22+x1x2>0,
,所以x1-x2<0.有x12+x22+x1x2>0,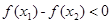 ,所以
,所以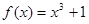 为R上的单调递增函数。
为R上的单调递增函数。