题目内容
(湖南省●2010年月考)如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1,M、N分别是A1B、B1C1的中点.

 (Ⅰ)求证:MN⊥平面A1BC;
(Ⅰ)求证:MN⊥平面A1BC;
 (Ⅱ)求直线BC1和平面A1BC所成角的大小.
(Ⅱ)求直线BC1和平面A1BC所成角的大小.



 (Ⅰ)求证:MN⊥平面A1BC;
(Ⅰ)求证:MN⊥平面A1BC; (Ⅱ)求直线BC1和平面A1BC所成角的大小.
(Ⅱ)求直线BC1和平面A1BC所成角的大小.

见解析
解法一:(Ⅰ)由已知BC⊥AC,BC⊥CC1,

 所以BC⊥平面ACC1A1.连结AC1,则BC⊥AC1.
所以BC⊥平面ACC1A1.连结AC1,则BC⊥AC1.

 由已知,侧面ACC1A1是正方形,所以A1C⊥AC1.
由已知,侧面ACC1A1是正方形,所以A1C⊥AC1.
 又
又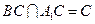 ,所以AC1⊥平面A1BC.
,所以AC1⊥平面A1BC.
 因为侧面ABB1A1是正方形,M是A1B的中点,连结AB1,则点M是AB1的中点.
因为侧面ABB1A1是正方形,M是A1B的中点,连结AB1,则点M是AB1的中点.
 又点N是B1C1的中点,则MN是△AB1C1的中位线,所以MN∥AC1. 故MN⊥平面A1BC.
又点N是B1C1的中点,则MN是△AB1C1的中位线,所以MN∥AC1. 故MN⊥平面A1BC.
 (Ⅱ)因为AC1⊥平面A1BC,设AC1与A1C相交于点D,
(Ⅱ)因为AC1⊥平面A1BC,设AC1与A1C相交于点D, 连结BD,则∠C1BD为直线BC1和平面A1BC所成角.
连结BD,则∠C1BD为直线BC1和平面A1BC所成角.
 设AC=BC=CC1=a,则
设AC=BC=CC1=a,则 ,
, .
.
 在Rt△BDC1中,sin∠C1BD=
在Rt△BDC1中,sin∠C1BD= ,
,
 所以∠C1BD=30º,故直线BC1和平面A1BC所成的角为30º.
所以∠C1BD=30º,故直线BC1和平面A1BC所成的角为30º.
 解法二:(Ⅰ)据题意CA、CB、CC1两两垂直,以C为原点,
解法二:(Ⅰ)据题意CA、CB、CC1两两垂直,以C为原点,
 CA、CB、CC1所在直线分别为x轴、y轴、z轴,建立空间
CA、CB、CC1所在直线分别为x轴、y轴、z轴,建立空间
 直角坐标系,如图
直角坐标系,如图 设AC=BC=CC1=a,则
设AC=BC=CC1=a,则

 ,
,

 ,
,
 所以
所以 ,
, ,
,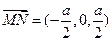 .
.
 于是
于是 ,
, ,即MN⊥BA1,MN⊥CA1.
,即MN⊥BA1,MN⊥CA1.
 又
又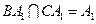 ,故MN⊥平面A1BC.
,故MN⊥平面A1BC.
 (Ⅱ)因为MN⊥平面A1BC,则
(Ⅱ)因为MN⊥平面A1BC,则 为平面A1BC的法向量,又
为平面A1BC的法向量,又 ,
,
 则
则 ,所以
,所以 .
.
 故直线BC1和平面A1BC所成的角为30º.
故直线BC1和平面A1BC所成的角为30º.

 所以BC⊥平面ACC1A1.连结AC1,则BC⊥AC1.
所以BC⊥平面ACC1A1.连结AC1,则BC⊥AC1. 
 由已知,侧面ACC1A1是正方形,所以A1C⊥AC1.
由已知,侧面ACC1A1是正方形,所以A1C⊥AC1.  又
又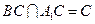 ,所以AC1⊥平面A1BC.
,所以AC1⊥平面A1BC.  因为侧面ABB1A1是正方形,M是A1B的中点,连结AB1,则点M是AB1的中点.
因为侧面ABB1A1是正方形,M是A1B的中点,连结AB1,则点M是AB1的中点. 又点N是B1C1的中点,则MN是△AB1C1的中位线,所以MN∥AC1. 故MN⊥平面A1BC.
又点N是B1C1的中点,则MN是△AB1C1的中位线,所以MN∥AC1. 故MN⊥平面A1BC.  (Ⅱ)因为AC1⊥平面A1BC,设AC1与A1C相交于点D,
(Ⅱ)因为AC1⊥平面A1BC,设AC1与A1C相交于点D, 连结BD,则∠C1BD为直线BC1和平面A1BC所成角.
连结BD,则∠C1BD为直线BC1和平面A1BC所成角.  设AC=BC=CC1=a,则
设AC=BC=CC1=a,则 ,
, .
.  在Rt△BDC1中,sin∠C1BD=
在Rt△BDC1中,sin∠C1BD= ,
,  所以∠C1BD=30º,故直线BC1和平面A1BC所成的角为30º.
所以∠C1BD=30º,故直线BC1和平面A1BC所成的角为30º.  解法二:(Ⅰ)据题意CA、CB、CC1两两垂直,以C为原点,
解法二:(Ⅰ)据题意CA、CB、CC1两两垂直,以C为原点, CA、CB、CC1所在直线分别为x轴、y轴、z轴,建立空间
CA、CB、CC1所在直线分别为x轴、y轴、z轴,建立空间 直角坐标系,如图
直角坐标系,如图 设AC=BC=CC1=a,则
设AC=BC=CC1=a,则
 ,
,
 ,
,
 所以
所以 ,
, ,
,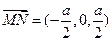 .
.  于是
于是 ,
, ,即MN⊥BA1,MN⊥CA1.
,即MN⊥BA1,MN⊥CA1.  又
又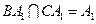 ,故MN⊥平面A1BC.
,故MN⊥平面A1BC.  (Ⅱ)因为MN⊥平面A1BC,则
(Ⅱ)因为MN⊥平面A1BC,则 为平面A1BC的法向量,又
为平面A1BC的法向量,又 ,
, 则
则 ,所以
,所以 .
. 故直线BC1和平面A1BC所成的角为30º.
故直线BC1和平面A1BC所成的角为30º.
练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
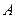 ,
,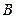 ,
,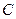 三点都是平面
三点都是平面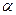 与平面
与平面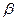 的公共点,并且
的公共点,并且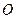 在二面角
在二面角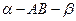 的棱上,点
的棱上,点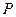 在
在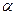 内,且
内,且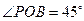 .若对于
.若对于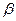 内异于
内异于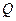 ,都有
,都有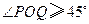 ,则二面角
,则二面角 如图,直三棱柱
如图,直三棱柱 中,
中, ,
, 上有一动点
上有一动点 ,则
,则 周长的最小值为
周长的最小值为
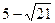


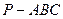 中,
中,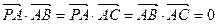 ,
,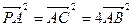 .
.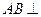 平面
平面 ;
; (Ⅱ)若
(Ⅱ)若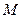 为线段
为线段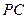 上的点,设
上的点,设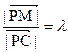 ,问
,问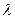 为何值时能使
为何值时能使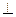 平面
平面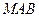 ;
;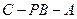 的大小.
的大小. 底面ABCD,当
底面ABCD,当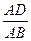 的值等于多少时,能使PB
的值等于多少时,能使PB
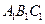 的底面边长均为2,侧棱
的底面边长均为2,侧棱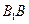 的长为2且与底面ABC所成角为
的长为2且与底面ABC所成角为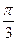 ,且侧面
,且侧面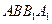 垂直于底面ABC.
垂直于底面ABC.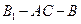 的正切值的大小;
的正切值的大小;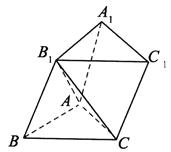 (2)若其余条件不变,只改变侧棱的长度,当侧棱
(2)若其余条件不变,只改变侧棱的长度,当侧棱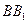 的长度为多长时,可使面
的长度为多长时,可使面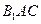 和底面垂直.
和底面垂直. 所在平面外一点,PA、PB、PC与平面ABC所的角均相等,又PA与BC垂直,那么
所在平面外一点,PA、PB、PC与平面ABC所的角均相等,又PA与BC垂直,那么