Question

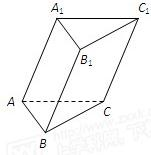如图，已知斜三棱柱ABC-A₁B₁C₁的底面边长分别是AB=AC=10cm，BC=12cm，侧棱AA₁=13cm，顶点A₁与下底面各个顶点的距离相等，求这个棱柱的全面积．

Answer 1

分析：说明顶点A₁ 在平面 ABC 上的射影为△ABC 的外心，通过数据关系求出几何体的侧面积，上下底面面积，然后求出全面积．

解答：解：∵A₁A=A₁B=A₁C
∴点 A₁ 在平面 ABC 上的射影为△ABC 的外心，在∠BAC 平分线 AD 上
∵AB=AC
∴AD⊥BC
∵AD 为 A₁A 在平面 ABC 上的射影 
∴BC⊥AA₁
∴BC⊥BB₁
∴BB₁C₁C 为矩形，S=BB₁×BC=156 取 AB 中点 E，连 A₁E
∵A₁A=A₁B
∴A₁E⊥AB
∴A₁E=12
∴S_AA1C1C=S_AA1B1B=120
∴S_侧=396
 S_全=S_侧+2×

1

2

×12×8=396+96=492（cm²）
这个棱柱的全面积为492cm²

点评：本题考查棱柱的表面积，考查空间想象能力，逻辑推理计算能力，点 A₁ 在平面 ABC 上的射影为△ABC 的外心，在∠BAC 平分线 AD 上，是解题的关键；是基础题．