题目内容
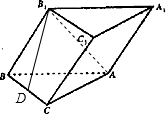
 (2012•梅州二模)如图,已知斜三棱柱ABC-A1B1C1中,点B1在底面ABC上的射影落在BC上,CA=CB=a,AB=
(2012•梅州二模)如图,已知斜三棱柱ABC-A1B1C1中,点B1在底面ABC上的射影落在BC上,CA=CB=a,AB=| 2 |
(1)求证:AC⊥平面BCC1B1;
(2)当BB1与底面ABC所成的角为60°,且AB1⊥BC1时,求点B1到平面AC1的距离.
分析:(1)先证明AC⊥BC,利用点B1在底面ABC上的射影落在BC上,可得侧面BCC1B1⊥底面ABC,从而可得AC⊥平面BCC1B1;
(2)先证明B1BC是等边三角形,取BC的中点D,连接B1D,则B1D为三棱柱的高,利用等体积可求点B1到平面AC1的距离.
(2)先证明B1BC是等边三角形,取BC的中点D,连接B1D,则B1D为三棱柱的高,利用等体积可求点B1到平面AC1的距离.
解答:(1)证明:∵CA=CB=a,AB=
a,∴AB2=CA2+CB2,∴AC⊥BC
∵点B1在底面ABC上的射影落在BC上,
∴侧面BCC1B1⊥底面ABC,
∵侧面BCC1B1∩底面ABC=BC
∴AC⊥平面BCC1B1;
(2)解:∵点B1在底面ABC上的射影落在BC上,
∴∠B1BC=60°
∵AC⊥平面BCC1B1
∴BC1⊥AC
∵AB1⊥BC1,AB1∩AC=A
∴BC1⊥平面AB1C
∴BC1⊥B1C
∵BCC1B1是平行四边形,∴BCC1B1是菱形
∴△B1BC是等边三角形
取BC的中点D,连接B1D,则B1D⊥BC
∵侧面BCC1B1⊥底面ABC,
∴B1D⊥底面ABC,
∴B1D为三棱柱的高,B1D=
a,S△ABC=
∴VABC-A1B1C1=
∴VB1-ACC1A1=
VABC-A1B1C1=
∵AC⊥平面BCC1B1
∴CC1⊥AC
∴四边形ACC1A1是边长为a的正方形
设点B1到平面AC1的距离为d,则有
da2=
,∴d=
a
∴点B1到平面AC1的距离为
a.
| 2 |
∵点B1在底面ABC上的射影落在BC上,
∴侧面BCC1B1⊥底面ABC,
∵侧面BCC1B1∩底面ABC=BC
∴AC⊥平面BCC1B1;
(2)解:∵点B1在底面ABC上的射影落在BC上,

∴∠B1BC=60°
∵AC⊥平面BCC1B1
∴BC1⊥AC
∵AB1⊥BC1,AB1∩AC=A
∴BC1⊥平面AB1C
∴BC1⊥B1C
∵BCC1B1是平行四边形,∴BCC1B1是菱形
∴△B1BC是等边三角形
取BC的中点D,连接B1D,则B1D⊥BC
∵侧面BCC1B1⊥底面ABC,
∴B1D⊥底面ABC,
∴B1D为三棱柱的高,B1D=
| ||
| 2 |
| a2 |
| 2 |
∴VABC-A1B1C1=
| ||
| 4 |
∴VB1-ACC1A1=
| 2 |
| 3 |
| ||
| 6 |
∵AC⊥平面BCC1B1
∴CC1⊥AC
∴四边形ACC1A1是边长为a的正方形
设点B1到平面AC1的距离为d,则有
| 1 |
| 3 |
| ||
| 6 |
| ||
| 2 |
∴点B1到平面AC1的距离为
| ||
| 2 |
点评:本题考查线面垂直,考查点到面的距离,掌握面面垂直的性质,正确求体积是关键.

练习册系列答案
相关题目
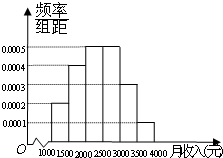 (2012•梅州二模)一个社会调查机构就某社区居民的月收入调查了10 000人,并根据所得数据画了样本的频率分布直方图(如图).
(2012•梅州二模)一个社会调查机构就某社区居民的月收入调查了10 000人,并根据所得数据画了样本的频率分布直方图(如图).