Question

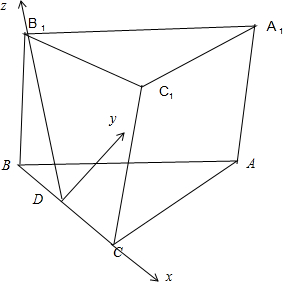
（2011•孝感模拟）如图，已知斜三棱柱ABC-A₁B₁C₁的底面是直角三角形，∠ACB=90°，侧棱与底面所成的角为θ，且
AB₁⊥BC₁，点B₁在底面上的射影D在BC上．
（I）若D点是BC的中点，求θ；
（Ⅱ）若cosθ=

1

3

，且AC=BC=AA₁=a，求二面角C-AB-C₁的大小．

Answer 1

分析：（I）点D恰为BC中点，且AB₁⊥BC₁，得到B₁D⊥平面ABC；作出侧棱与底面所成角，然后求θ的大小；
（II）建立空间直角坐标系，利用向量的数量积求二面角C-AB-C₁的大小．

解答：解；（I）∵AB₁⊥BC₁，AC⊥BC₁，AB₁与AC相交A，
∴BC₁⊥平面AB₁C，
B₁C?平面AB₁C⇒BC₁⊥B₁C
∴四边形BB₁C₁C为菱形，（5分）
又∵D为BC的中点，B₁D⊥平面ABC
∴∠B₁BC为侧棱和底面所成的角α，
∴cos∠B₁BC=

BD

BB 1

=

1

2

．
∴∠B₁BC=60°，即侧棱与底面所成角60°．（8分）
（II）以CD为x轴，DB₁为Z轴，过D点且平行于AC的直线为y轴，建立空间直角坐标系，
∵B₁D⊥平面ABC，
∴cosθ=cos∠B₁BD=

BD

BB 1

=

1

3

，
∴BD=

a

3

，
∴B₁D=

a 2- 1 9 a 2

=

2 2

3

a．
∴则A（

2

3

a，a，0），B（-

1

3

a，0，0），C（

2a

3

，0，0），B₁（0，0，

2 2 a

3

），C₁（a，0，

2 2

3

a）．
所以：平面ABC的法向量

DB 1

=（0，0，

2 2 a

3

），
设平面ABC₁的法向量为

n

=（x，y，z），
由

n • BA  =0 n •  BC 1 =0

⇒

ax+ay=0 4 3 ax+ 2 2 ax 3 =0

，
∴y=-x，z=-

2

x．
令x=1得

n

=（1，-1，-

2

）
∴cos＜

n

，

DB 1

＞=

- 4 3 a

2× 2 2 a 3

=-

2

2

，
∵二面角C-AB-C₁大小是锐二面角，
∴二面角C-AB-C₁的大小是45°（12分）

点评：本题考查直线与平面垂直的判定，线面角和二面角的求法，考查空间想象能力、逻辑思维能力，是中档题．