题目内容
 如图,已知斜三棱柱ABC-A1B1C1的各棱长均为2,侧棱与底面所成角为
如图,已知斜三棱柱ABC-A1B1C1的各棱长均为2,侧棱与底面所成角为| π | 3 |
(1)求证:侧面ABB1A1⊥底面ABC;
(2)证明:B1C⊥C1A;
(3)求二面角B1-BC-A的大小.
分析:(1)通过直线与平面垂直的判定定理,利用平面与平面垂直的判定定理证明:侧面ABB1A1⊥底面ABC;
(2)通过证明B1C⊥面ABC1,然后证明B1C⊥C1A;
(3)作DE⊥BC于E,连B1E,则由三垂线定理知:B1E⊥BC,说明∠B1ED为二面角B1-BC-A的平面角,通过解三角形求二面角B1-BC-A的大小.
(2)通过证明B1C⊥面ABC1,然后证明B1C⊥C1A;
(3)作DE⊥BC于E,连B1E,则由三垂线定理知:B1E⊥BC,说明∠B1ED为二面角B1-BC-A的平面角,通过解三角形求二面角B1-BC-A的大小.
解答: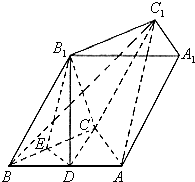 解:(1)依题意:
解:(1)依题意:
∵顶点B1在底面ABC上的射影D在AB上.
∴B1D⊥面ABC,且B1D?面ABB1A1
∴面ABB1A1⊥面ABC
(2)连BC1、CD
∵B1D⊥面ABC,∴∠B1BD=
∴BD=B1Dcos
=1,即D为AB中点
∴CD⊥AB
又AB⊥B1D,CD∩B1D=D
∴AB⊥面B1DC,又B1C?面B1DC
∴AB⊥B1C
∵四边形B1BCC1是菱形∴B1C⊥BC1
又AB∩BC1=B,∴B1C⊥面ABC1
∵C1A?面ABC1∴B1C⊥C1A
(3)作DE⊥BC于E,连B1E,则由三垂线定理知:B1E⊥BC
∴∠B1ED为二面角B1-BC-A的平面角
∴∠B1ED=arctan2,即二面角B1-BC-A为arctan2
 解:(1)依题意:
解:(1)依题意:∵顶点B1在底面ABC上的射影D在AB上.
∴B1D⊥面ABC,且B1D?面ABB1A1
∴面ABB1A1⊥面ABC
(2)连BC1、CD
∵B1D⊥面ABC,∴∠B1BD=
| π |
| 3 |
| π |
| 3 |
∴CD⊥AB
又AB⊥B1D,CD∩B1D=D
∴AB⊥面B1DC,又B1C?面B1DC
∴AB⊥B1C
∵四边形B1BCC1是菱形∴B1C⊥BC1
又AB∩BC1=B,∴B1C⊥面ABC1
∵C1A?面ABC1∴B1C⊥C1A
(3)作DE⊥BC于E,连B1E,则由三垂线定理知:B1E⊥BC
∴∠B1ED为二面角B1-BC-A的平面角
|
∴∠B1ED=arctan2,即二面角B1-BC-A为arctan2
点评:本题考查平面与平面垂直,直线与平面垂直的性质定理以及二面角的平面角的求法,考查空间想象能力以及计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (甲)如图,已知斜三棱柱ABC-A1B1C1的侧面A1C⊥底面ABC,∠ABC=90°,BC=2,AC=
(甲)如图,已知斜三棱柱ABC-A1B1C1的侧面A1C⊥底面ABC,∠ABC=90°,BC=2,AC= 如图,已知斜三棱柱ABC-A1B1C1的各棱长均为2,侧棱与底面所成的角为
如图,已知斜三棱柱ABC-A1B1C1的各棱长均为2,侧棱与底面所成的角为 (2011•孝感模拟)如图,已知斜三棱柱ABC-A1B1C1的底面是直角三角形,∠ACB=90°,侧棱与底面所成的角为θ,且
(2011•孝感模拟)如图,已知斜三棱柱ABC-A1B1C1的底面是直角三角形,∠ACB=90°,侧棱与底面所成的角为θ,且 (2012•梅州二模)如图,已知斜三棱柱ABC-A1B1C1中,点B1在底面ABC上的射影落在BC上,CA=CB=a,AB=
(2012•梅州二模)如图,已知斜三棱柱ABC-A1B1C1中,点B1在底面ABC上的射影落在BC上,CA=CB=a,AB=