��Ŀ����
 ���ף���ͼ����֪б������ABC-A1B1C1�IJ���A1C�͵���ABC����ABC=90�㣬BC=2��AC=2
���ף���ͼ����֪б������ABC-A1B1C1�IJ���A1C�͵���ABC����ABC=90�㣬BC=2��AC=2| 3 |
��1�������A1A�����ABC���ɵĽǵĴ�С��
��2�������A1B��������ɶ���ǵĴ�С��
��3�����C������A1B�ľ��룮
���ң����ⳤΪa��������OABC-O'A'B'C'�У�E��F�ֱ�����AB��BC�ϵĶ��㣬��AE=BF��
��1����֤��A'F��C'E��
��2��������B'-BEF�����ȡ�����ֵʱ��������B'-EF-B�Ĵ�С������÷����Ǻ�����ʾ����
�������ף�1�������⻭��ͼ�����ڲ���A1C�͵���ABC������A1A�����ABC���ɵĽ�Ϊ��A1AC��������ɣ�
��2�������⼰ͼ�����ö����ƽ��ǵĸ���������̵Ĵ�С��
��3�����������������ĵ���������ֻ��ɵþ��룮
�ң�1�����ڼ�����Ϊ�����壬�������������ռ�ֱ������ϵ��д��������Ŀռ���������������֪ʶ�͵������������룻
��2����������������ͼ�����ö���ǵ�ƽ��ǵĶ��壬���BF=x��BE=y����x+y=a�����þ�ֵ����ʽ���BE��BF�ij��ȣ������������н�����������ǵĴ�С��
��2�������⼰ͼ�����ö����ƽ��ǵĸ���������̵Ĵ�С��
��3�����������������ĵ���������ֻ��ɵþ��룮
�ң�1�����ڼ�����Ϊ�����壬�������������ռ�ֱ������ϵ��д��������Ŀռ���������������֪ʶ�͵������������룻
��2����������������ͼ�����ö���ǵ�ƽ��ǵĶ��壬���BF=x��BE=y����x+y=a�����þ�ֵ����ʽ���BE��BF�ij��ȣ������������н�����������ǵĴ�С��
������ף���1���߲���A1C�͵���ABC����A1A��ƽ��ABC�ϵ���Ӱ��AC��A1A�����ABC���ɵĽ�Ϊ��A1AC��
��A1A=A1C��A1A��A1C�����A1AC=45�㣮
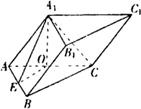 ��2����A1O��AC��O����A1O��ƽ��ABC������OE��AB��E������A1E����A1E��AB��
��2����A1O��AC��O����A1O��ƽ��ABC������OE��AB��E������A1E����A1E��AB��
���ԡ�A1EO���Dz���A1B�����ABC���ɶ���ǵ�ƽ��ǣ�
��Rt��A1EO��A1O=
AC=
��OE=
BC=1��
��tan��A1EO=
=
����A1EO=60�㣮
��3�����C������A1B�ľ���Ϊx��
��VA1-ABC=VC-A1BC��
��
•A1O•S��ABC=
•x•S��A1BC?A1O•S��ABC=x•S��ABC����*��
��A1O=
��OE=1����A1E=
=2��
��AB=
=2
����S��A1AB=
•2
•2=2
��
��S��ABC=
��2��2
=2
�����ɣ�*��ʽ����2
=x•2
=1����x=1
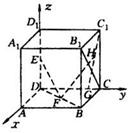 ���ң���1��֤������ͼ����OΪԭ�㽨���ռ�ֱ������ϵ��
���ң���1��֤������ͼ����OΪԭ�㽨���ռ�ֱ������ϵ��
��AE=BF=x����A'��a��0��a����F��a-x��a��0����C'��0��a��a����E��a��x��0����
��
=��-x��a��-a����
=��a��x-a��-a����
��
•
=-xa+a(x-a)+a2=0��
��A'F��C'E��
��2���⣺��BF=x��BE=y����x+y=a��������B'-BEF�����ΪV=
xya��
(
)2=
a2��
���ҽ���x=y=
ʱ���Ⱥų�������ˣ�����B'-BEF�����ȡ�����ֵʱ��BE=BF=
��
��B��BD��BF��EF��D������B'D����B'D��EF��
���B'DB�Ƕ����B'-EF-B��ƽ��ǣ���Rt��BEF�У�ֱ�DZ�BE=BF=
��BD��б���ϵĸߣ���BD=
��Rt��B'DB��tan��B��DB=
=2
���ʶ����B'-EF-B�Ĵ�СΪarctan2
��
��A1A=A1C��A1A��A1C�����A1AC=45�㣮
 ��2����A1O��AC��O����A1O��ƽ��ABC������OE��AB��E������A1E����A1E��AB��
��2����A1O��AC��O����A1O��ƽ��ABC������OE��AB��E������A1E����A1E��AB�����ԡ�A1EO���Dz���A1B�����ABC���ɶ���ǵ�ƽ��ǣ�
��Rt��A1EO��A1O=
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
��tan��A1EO=
| A1O |
| OE |
| 3 |
��3�����C������A1B�ľ���Ϊx��
��VA1-ABC=VC-A1BC��
��
| 1 |
| 3 |
| 1 |
| 3 |
��A1O=
| 3 |
| 3+1 |
��AB=
(2
|
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
��S��ABC=
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
 ���ң���1��֤������ͼ����OΪԭ�㽨���ռ�ֱ������ϵ��
���ң���1��֤������ͼ����OΪԭ�㽨���ռ�ֱ������ϵ����AE=BF=x����A'��a��0��a����F��a-x��a��0����C'��0��a��a����E��a��x��0����
��
| A��F |
| C��E |
��
| A��F |
| C��E |
��A'F��C'E��
��2���⣺��BF=x��BE=y����x+y=a��������B'-BEF�����ΪV=
| 1 |
| 6 |
| a |
| b |
| x+y |
| 2 |
| 1 |
| 24 |
���ҽ���x=y=
| a |
| 2 |
| a |
| 2 |
��B��BD��BF��EF��D������B'D����B'D��EF��
���B'DB�Ƕ����B'-EF-B��ƽ��ǣ���Rt��BEF�У�ֱ�DZ�BE=BF=
| a |
| 2 |
| ||
| 4 |
��Rt��B'DB��tan��B��DB=
| B��B |
| BD |
| 2 |
| 2 |
�������ף�1�������ص㿼�������洹ֱ�����ʶ���������ǵĶ��壻
��2�������ص㿼���˶���ǵ�ƽ��ǵĸ��������������������εĽǵĴ�С��
��3�������ص㿼�������������ĵ�������Խ��ж����ֻ������������������㵽��ľ��룮
�ң�1�������ص㿼�������ó�������ص㽨���ռ�ֱ������ϵ������������֪ʶ������ߴ�ֱ��֤����
��2�������ص㿼��������������֪ʶ������������þ�ֵ����ʽ�������ֵʱ���߶γ��ȣ�������������ǵĴ�С���������˷����ǵ�֪ʶ��
��2�������ص㿼���˶���ǵ�ƽ��ǵĸ��������������������εĽǵĴ�С��
��3�������ص㿼�������������ĵ�������Խ��ж����ֻ������������������㵽��ľ��룮
�ң�1�������ص㿼�������ó�������ص㽨���ռ�ֱ������ϵ������������֪ʶ������ߴ�ֱ��֤����
��2�������ص㿼��������������֪ʶ������������þ�ֵ����ʽ�������ֵʱ���߶γ��ȣ�������������ǵĴ�С���������˷����ǵ�֪ʶ��

��ϰ��ϵ�д�
 �¿α�����Ķ�ѵ��ϵ�д�
�¿α�����Ķ�ѵ��ϵ�д�
�����Ŀ
 ����AA1��A1C��AA1=A1C��
����AA1��A1C��AA1=A1C��