题目内容
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设![]() 为曲线
为曲线![]() 上的点,
上的点,![]() ,垂足为
,垂足为![]() ,若
,若![]() 的最小值为
的最小值为![]() ,求
,求![]() 的值.
的值.
【答案】(Ⅰ)![]() ,
,![]() ;(Ⅱ)
;(Ⅱ)![]() 或
或![]() .
.
【解析】
(Ⅰ)消去参数![]() 可得直线
可得直线![]() 的普通方程,利用互化公式即可得曲线
的普通方程,利用互化公式即可得曲线![]() 的直角坐标方程.
的直角坐标方程.
(Ⅱ)利用曲线![]() 的参数方程设点
的参数方程设点![]() ,根据点到直线距离公式求出
,根据点到直线距离公式求出![]() ,再根据三角函数性质求出最小值,利用已知列方程可解得
,再根据三角函数性质求出最小值,利用已知列方程可解得![]() .
.
(Ⅰ)因为曲线![]() 的极坐标方程为
的极坐标方程为![]() ,即
,即![]() ,
,
将![]() ,
,![]() 代入上式并化简得
代入上式并化简得![]() ,
,
所以曲线![]() 的直角坐标方程为
的直角坐标方程为![]() ,
,
消去参数![]() 可得直线
可得直线![]() 的普通方程为
的普通方程为![]() .
.
(Ⅱ)设![]() ,由点到直线的距离公式得
,由点到直线的距离公式得
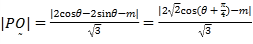 ,
,
由题意知![]() ,
,
当![]() 时,
时,![]() ,得
,得![]() ,
,
当![]() 时,|
时,|![]() ,得
,得![]() ;
;
所以![]() 或
或![]() .
.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
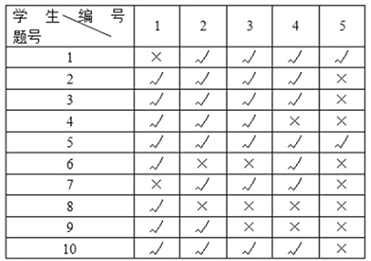
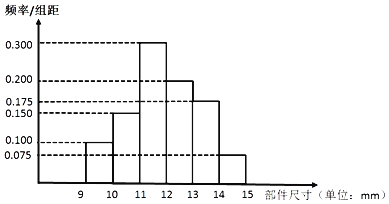
【题目】某校在高一年级一班至六班进行了“社团活动”满意度调查(结果只有“满意”和“不满意”两种),从被调查的学生中随机抽取了50人,具体的调查结果如表:
班号 | 一班 | 二班 | 三班 | 四班 | 五班 | 六班 |
频数 | 4 | 5 | 11 | 8 | 10 | 12 |
满意人数 | 3 | 2 | 8 | 5 | 6 | 6 |
现从一班和二班调查对象中随机选取4人进行追踪调查,则选中的4人中恰有2人不满意的概率为___________;若将以上统计数据中学生持满意态度的频率视为概率,在高一年级全体学生中随机抽取3名学生,记其中满意的人数为X,则随机变量X的数学期望是___________