题目内容
(本小题满分12分)
已知椭圆C: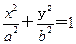 (a>b>0)的离心率为
(a>b>0)的离心率为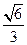 ,其左、右焦点分别是F1、F2,点P是坐标平面内的一点,且|OP|=
,其左、右焦点分别是F1、F2,点P是坐标平面内的一点,且|OP|=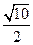 ,
,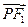 ·
·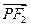 =
=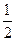 (点O为坐标原点).
(点O为坐标原点).
(Ⅰ)求椭圆C的方程;
(Ⅱ)直线y=x与椭圆C在第一象限交于A点,若椭圆C上两点M、N使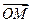 +
+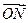 =
=
λ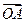 ,λ∈(0,2)求△OMN面积的最大值.
,λ∈(0,2)求△OMN面积的最大值.
已知椭圆C:
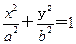 (a>b>0)的离心率为
(a>b>0)的离心率为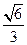 ,其左、右焦点分别是F1、F2,点P是坐标平面内的一点,且|OP|=
,其左、右焦点分别是F1、F2,点P是坐标平面内的一点,且|OP|=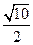 ,
,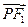 ·
·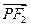 =
=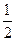 (点O为坐标原点).
(点O为坐标原点).(Ⅰ)求椭圆C的方程;
(Ⅱ)直线y=x与椭圆C在第一象限交于A点,若椭圆C上两点M、N使
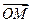 +
+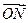 =
=λ
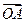 ,λ∈(0,2)求△OMN面积的最大值.
,λ∈(0,2)求△OMN面积的最大值.解:(Ⅰ)设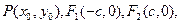 则由
则由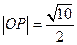 得
得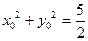 ,
,
由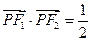 得
得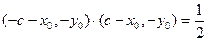 ,即
,即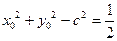 ………2分
………2分
所以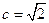 ,又因为
,又因为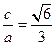 ,所以
,所以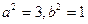 ………3分
………3分
椭圆C的方程为: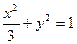 ; ……….4分
; ……….4分
(Ⅱ)解法一:由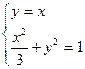 得
得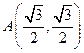 ,
,
设直线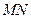 的方程为
的方程为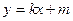 ,联立
,联立 方程组
方程组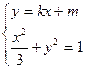
消去y得: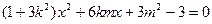 ………5分
………5分
设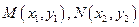 ,
,
则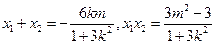 ………6分
………6分
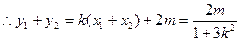
∵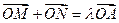 ,∴
,∴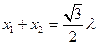 ,
,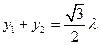
得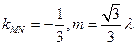 ,于是
,于是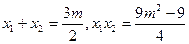 ………8分
………8分
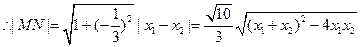
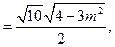 ………9分
………9分
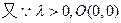 到直线
到直线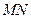 的距离为
的距离为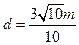
∴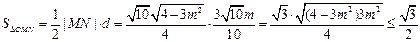 ,
,
当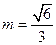 ,即
,即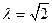 时等号成立,
时等号成立,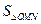 的最大值为
的最大值为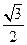 ………12分
………12分
解法二:由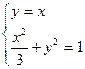 得
得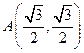 ,
,
设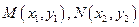 则
则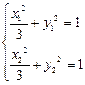
∴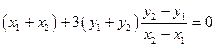 …………① ………5分
…………① ………5分
∵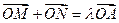 ,
,
∴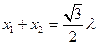 ,
,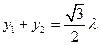 代入①得
代入①得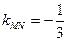 , ………6分
, ………6分
设直线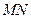 的方程为
的方程为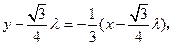
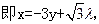 ………7分
………7分
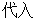 椭圆方程得
椭圆方程得 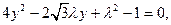
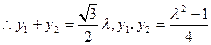 ,
,
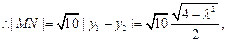
 ……….9分
……….9分
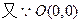 到直线
到直线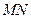 的距离为
的距离为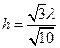
∴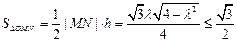 , ………11分
, ………11分
当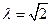 时等号成立,
时等号成立,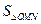 的最大值为
的最大值为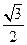 ………12分
………12分
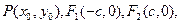 则由
则由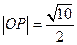 得
得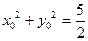 ,
,由
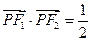 得
得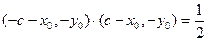 ,即
,即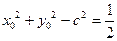 ………2分
………2分所以
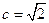 ,又因为
,又因为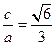 ,所以
,所以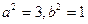 ………3分
………3分椭圆C的方程为:
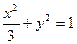 ; ……….4分
; ……….4分(Ⅱ)解法一:由
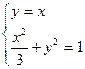 得
得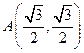 ,
,设直线
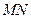 的方程为
的方程为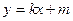 ,联立
,联立 方程组
方程组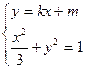
消去y得:
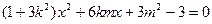 ………5分
………5分设
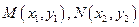 ,
,则
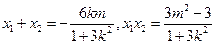 ………6分
………6分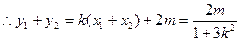
∵
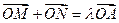 ,∴
,∴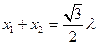 ,
,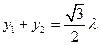
得
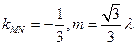 ,于是
,于是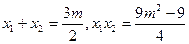 ………8分
………8分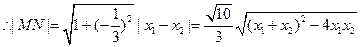
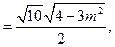 ………9分
………9分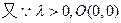 到直线
到直线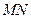 的距离为
的距离为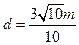
∴
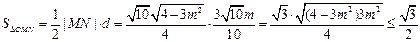 ,
,当
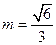 ,即
,即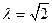 时等号成立,
时等号成立,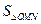 的最大值为
的最大值为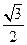 ………12分
………12分解法二:由
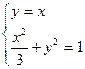 得
得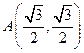 ,
,设
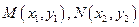 则
则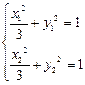
∴
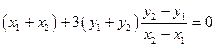 …………① ………5分
…………① ………5分∵
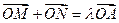 ,
,∴
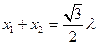 ,
,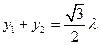 代入①得
代入①得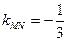 , ………6分
, ………6分设直线
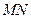 的方程为
的方程为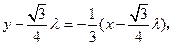
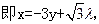 ………7分
………7分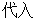 椭圆方程得
椭圆方程得 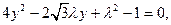
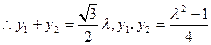 ,
,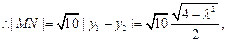
 ……….9分
……….9分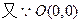 到直线
到直线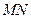 的距离为
的距离为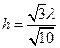
∴
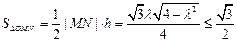 , ………11分
, ………11分当
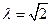 时等号成立,
时等号成立,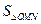 的最大值为
的最大值为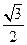 ………12分
………12分略

练习册系列答案
相关题目
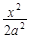 +
+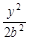 =1(a>b>0)与双曲线
=1(a>b>0)与双曲线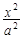 -
-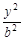 =1有相同的焦点,则椭圆的离心率为
=1有相同的焦点,则椭圆的离心率为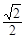

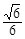
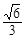
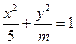 表示是焦点在y轴上的椭圆;q:三次函数
表示是焦点在y轴上的椭圆;q:三次函数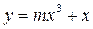
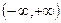 内单调递增,.求使“
内单调递增,.求使“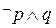 ”为真命题的实数m的取值范围.
”为真命题的实数m的取值范围.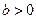 ,椭圆方程为
,椭圆方程为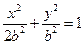 ,抛物线方程为
,抛物线方程为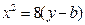 .如图所示,过点
.如图所示,过点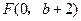 作
作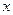 轴的平行线,与抛物线在第一象限的交点为
轴的平行线,与抛物线在第一象限的交点为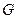 ,已知抛物线在点
,已知抛物线在点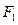 .
.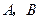 分别是椭圆长轴的左、右端点,试探究在抛物线上是否存在点
分别是椭圆长轴的左、右端点,试探究在抛物线上是否存在点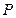 ,使得
,使得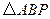 为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).
为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).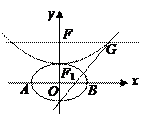
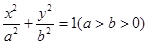 与双曲线
与双曲线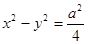 有相同的焦点,则椭圆的离心率为 ( )
有相同的焦点,则椭圆的离心率为 ( )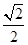
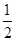
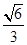

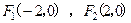 ,则这个椭圆的离心率等于_________________:
,则这个椭圆的离心率等于_________________: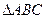 中,∠ABC=450,∠ACB=600,
中,∠ABC=450,∠ACB=600, ,记以AC为母线的圆锥为M2,m是圆锥M1任一母线,则圆锥M2的母线中与m垂直的直线有 ▲ 条
,记以AC为母线的圆锥为M2,m是圆锥M1任一母线,则圆锥M2的母线中与m垂直的直线有 ▲ 条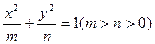 和双曲线
和双曲线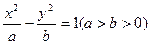 有相同的左、右焦点
有相同的左、右焦点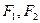 ,P是两条曲线的一个交点,则
,P是两条曲线的一个交点,则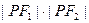 的值是( ).
的值是( ).
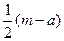


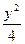 =1上的动点,则x+2y的最大值为 .
=1上的动点,则x+2y的最大值为 .