题目内容
14.在正三角形ABC中,E、F、P分别是-AB、AC、BC边上的点,满足AE:EB=CF:FA=CP:PB=1:2(如图1).将△AEF沿EF折起到△A1EF的位置,使二面角A1-EF-B成直二面角,连结A1B、A1P(如图2).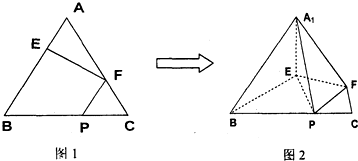
(1)求证:A1E⊥平面BEP;
(2)求二面角B一A1P一F的余弦值的大小.
分析 (1)利用线面垂直的判定定理即可证明A1E⊥平面BEP;
(2)建立空间坐标系,求出平面的法向量,利用向量法即可求二面角B一A1P一F的余弦值的大小.
解答  解:不妨设正三角形ABC 的边长为 3.
解:不妨设正三角形ABC 的边长为 3.
(1)在图1中,取BE的中点D,连结DF.
∵AE:EB=CF:FA=1:2,
∴AF=AD=2.…(2分)
而∠A=60°,∴△ADF是正三角形.
又AE=DE=1,∴EF⊥AD.…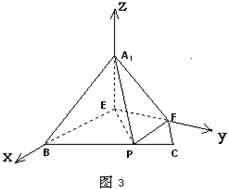 (4分)
(4分)
在图2中,A1E⊥EF,BE⊥EF,
∴∠A1EB为二面角A1-EF-B的平面角.
由题设条件知此二面角为直二面角,
∴A1E⊥BE.又BE∩EF=E,
∴A1E⊥平面BEF,即A1E⊥平面BEP.…(6分)
(2)由(1)知,即A1E⊥平面BEP,BE⊥EF.
以E为原点,以EB、EF、EA1分别为x、y、z轴建立如图3所示的坐标系如图,…(7分)
$则{A_1}(0,0,1),B(2,0,0),F(0,\sqrt{3},0),P(1,\sqrt{3},0)$.…(8分)
∴$\overrightarrow{{A_1}B}=(2,0,-1),\overrightarrow{{A_1}P}=(1,\sqrt{3},-1),\overrightarrow{{A_1}F}=(0,\sqrt{3},-1)$.…(9分)$设\overrightarrow m=({x_1},{y_1},{z_1}),\overrightarrow n=({x_2},{y_2},{z_2})分别是平面{A_1}BP和平面{A_1}PF的法向量$,
$由\left\{\begin{array}{l}\overrightarrow m•\overrightarrow{{A_1}B}=0\\ \overrightarrow m•\overrightarrow{{A_1}P}=0.\end{array}\right.得\left\{\begin{array}{l}2{x_1}-{z_1}=0\\{x_1}+\sqrt{3}{y_1}-{z_1}=0.\end{array}\right.$…(10分),
$取{y_1}=1,得\overrightarrow m=(\sqrt{3},1,2\sqrt{3})$.…(11分),
$由\left\{\begin{array}{l}\overrightarrow n•\overrightarrow{{A_1}F}=0\\ \overrightarrow m•\overrightarrow{{A_1}P}=0.\end{array}\right.得\left\{\begin{array}{l}\sqrt{3}{y_2}-{z_2}=0\\{x_2}+\sqrt{3}{y_2}-{z_2}=0.\end{array}\right.$$取{y_2}=1,得\overrightarrow n=(0,1,\sqrt{3})$.…(12分),
$所以cos<\overrightarrow m,\overrightarrow n>=\frac{\overrightarrow m•\overrightarrow n}{|\overrightarrow m||\overrightarrow n|}=\frac{7}{8}$.…(13分)
因为二面角B-A1P-F为钝角,$所以二面角B-{A_1}P-F的余弦值为-\frac{7}{8}$.…(14分)
点评 本题主要考查空间线面垂直的判定以及二面角的求解,建立坐标系,利用向量法是解决本题的关键.

 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案| A. | $\frac{1}{3}$ | B. | 3 | C. | $\frac{1}{2}$ | D. | 2 |
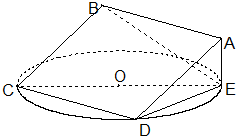 如图,正方形ABCD所在平面与圆O所在平面相交于CD,CE为圆O的直径,线段CD为圆O的弦,AE垂直于圆O所在平面.
如图,正方形ABCD所在平面与圆O所在平面相交于CD,CE为圆O的直径,线段CD为圆O的弦,AE垂直于圆O所在平面.