题目内容
4.设数列满足a1=3,(2-an)•an+1=1,则数列{an}的通项公式是an=$\frac{2n-5}{2n-3}$.分析 通过写出前几项猜测通项公式,然后利用数学归纳法证明即可.
解答 解:∵a1=3,(2-an)•an+1=1,
∴an+1=$\frac{1}{2-{a}_{n}}$,
∴a2=$\frac{1}{2-3}$=-1,a3=$\frac{1}{2-(-1)}$=$\frac{1}{3}$,a4=$\frac{1}{2-\frac{1}{3}}$=$\frac{3}{5}$,
…
猜想:数列{an}的通项公式an=$\frac{2n-5}{2n-3}$.
下面用数学归纳法证明:
当n=1时,显然成立;
假设当n=k时,有ak=$\frac{2k-5}{2k-3}$,
∵(2-an)•an+1=1,
∴ak+1=$\frac{1}{2-{a}_{k}}$=$\frac{1}{2-\frac{2k-5}{2k-3}}$=$\frac{1}{\frac{2k-1}{2k-3}}$=$\frac{2k-3}{2k-1}$=$\frac{2(k+1)-5}{2(k+1)-3}$,
即当n=k+1时也成立,
故数列{an}的通项公式an=$\frac{2n-5}{2n-3}$.
点评 本题考查求数列的通项,考查数学归纳法,注意解题方法的积累,属于中档题.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
12.已知x1、x2是函数f(x)=|lnx|-e-x的两个零点,则x1x2所在区间是( )
| A. | (0,$\frac{1}{e}$) | B. | ($\frac{1}{e}$,1) | C. | (1,2) | D. | (2,e) |
19.已知ω>0,0<φ<π,点A($\frac{π}{4}$,0)和点B($\frac{5π}{4}$,0)是函数f(x)=sin(ωx+φ)的图象的两个相邻的对称中心,则φ=( )
| A. | $\frac{π}{4}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{3π}{4}$ |
12.已知椭圆与双曲线$\frac{x^2}{3}-\frac{y^2}{2}=1$有共同的焦点,且离心率为$\frac{1}{{\sqrt{5}}}$,则椭圆的标准方程为( )
| A. | $\frac{x^2}{20}+\frac{y^2}{25}=1$ | B. | $\frac{x^2}{25}+\frac{y^2}{20}=1$ | C. | $\frac{x^2}{25}+\frac{y^2}{5}=1$ | D. | $\frac{x^2}{5}+\frac{y^2}{25}=1$ |

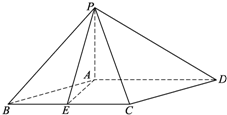 已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为菱形,∠ABC=60°,AB=2PA,E是线段BC的中点.
已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为菱形,∠ABC=60°,AB=2PA,E是线段BC的中点.