已知等差数列{an}的公差d≠0.若a1.a3.a9成等比数列.那么公比为( )A．$\frac{1}{3}$B．3C．$\frac{1}{2}$D．2 题目和参考答案——青夏教育精英家教网—

题目内容

3．已知等差数列{a_n}的公差d≠0，若a₁，a₃，a₉成等比数列，那么公比为（　　）

A．

$\frac{1}{3}$

B．

C．

$\frac{1}{2}$

D．

分析由已知条件求出a₁=d，所以该等比数列的公比为d=$\frac{{a}_{1}+2d}{{a}_{1}}$，由此能求出结果．

解答解：∵{a_n}是等差数列，公差d≠0，a₁，a₃，a₉成等比数列，
∴a₃²=a₁a₉，
即（a₁+2d）²=a₁•（a₁+8d），
解得a₁=d，
∴该等比数列的公比为d=$\frac{{a}_{1}+2d}{{a}_{1}}$=$\frac{3d}{d}$=3．
故选：B．

点评本题考查等比数列的公比的求法，是基础题，解题时要注意等差数列的通项公式的合理运用．

练习册系列答案

14．在正三角形ABC中，E、F、P分别是-AB、AC、BC边上的点，满足AE：EB=CF：FA=CP：PB=1：2（如图1）．将△AEF沿EF折起到△A₁EF的位置，使二面角A₁-EF-B成直二面角，连结A₁B、A₁P（如图2）．

（1）求证：A₁E⊥平面BEP；
（2）求二面角B一A₁P一F的余弦值的大小．

11．在圆锥PO中，已知高PO=2，底面圆的半径为1；根据圆锥曲线的定义，下列四个图中的截面边界曲线分别为圆、椭圆、双曲线及抛物线，其中点M为所在母线的中点，O为底面圆的圆心，对于下面四个命题，正确的个数有（　　）

①圆的面积为$\frac{π}{4}$；
②椭圆的长轴长为$\sqrt{13}$；
③双曲线两渐近线的夹角为arcsin$\frac{4}{5}$；
④抛物线上的点$（\frac{\sqrt{5}}{2}，1）$，其焦点到准线的距离为$\frac{{\sqrt{5}}}{5}$．

18．在正三角形ABC中，E、F、P分别是-AB、AC、BC边上的点，满足AE：EB=CF：FA=CP：PB=1：2（如图1）．将△AEF沿EF折起到△A₁EF的位置，使二面角A₁-EF-B成直二面角，连结A₁B、A₁P（如图2）

（1）求证：FP∥平面A₁EB．
（2）求证：A₁E⊥平面BEP；
（3）求直线A₁E与平面A₁BP所成角的大小．

8．等边三角形ABC的两个顶点坐标分别为A（4，-6），B（-2，-6），求点C的坐标．

15．

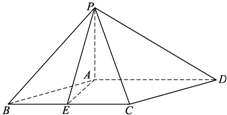已知四棱锥P-ABCD中，PA⊥平面ABCD，底面ABCD为菱形，∠ABC=60°，AB=2PA，E是线段BC的中点．
（1）求证：PE⊥AD；
（2）求平面PAE与平面PCD所成锐二面角的余弦值；
（3）在线段PD上是否存在一点F，使得CF∥平面PAE，并给出证明．

12．已知x₁、x₂是函数f（x）=|lnx|-e^-x的两个零点，则x₁x₂所在区间是（　　）

13．经过两点Q（1，1），P（4，3）的直线的参数方程，如果应用共线向量的充要条件来求，方程和参数的含义分别是x，y均为λ的一次函数，|λ|即为两向量的长度的比．

试题分类