题目内容
15.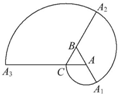 如图,△ABC是边长为1的正三角形,以A为圆心,AC为半径,沿逆时针方向画圆弧,交BA延长线于A1,记弧CA1的长为l1;以B为圆心,BA1为半径,沿逆时针方向画圆弧,交CB延长线于A2,记弧A1A2的长为l2;以C为圆心,CA2为半径,沿逆时针方向画圆弧,交AC延长线于A3,记弧A2A3的长为l3,则l1+l2+l3=4π.如此继续以A为圆心,AA3为半径,沿逆时针方向画圆弧,交AA1延长线于A4,记弧A3A4的长为l4,…,当弧长ln=8π时,n=12.
如图,△ABC是边长为1的正三角形,以A为圆心,AC为半径,沿逆时针方向画圆弧,交BA延长线于A1,记弧CA1的长为l1;以B为圆心,BA1为半径,沿逆时针方向画圆弧,交CB延长线于A2,记弧A1A2的长为l2;以C为圆心,CA2为半径,沿逆时针方向画圆弧,交AC延长线于A3,记弧A2A3的长为l3,则l1+l2+l3=4π.如此继续以A为圆心,AA3为半径,沿逆时针方向画圆弧,交AA1延长线于A4,记弧A3A4的长为l4,…,当弧长ln=8π时,n=12.
分析 根据弧长公式,分别求出l1、l2、l3,因此发现规律,进行归纳总结.
解答 解:由题意l1=$\frac{2}{3}π$,
l2=$\frac{4}{3}π$,
l3=$\frac{1}{3}×6π=2π$,
所以l1+l2+l3=4π;
l8=8π,即$\frac{2n}{3}π=8π$,解得n=12;
故答案为:4π;12.
点评 本题考查了归纳推理;关键是由具体的前三个弧长发现规律并进行猜测总结.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.设点P(x,y),则“x=1且y=-2”是“点P在直线l:x-y-3=0上”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
20.已知sin($\frac{π}{2}$+α)=$\frac{3}{5}$,则cos2α等于( )
| A. | $\frac{9}{25}$ | B. | -$\frac{9}{25}$ | C. | $\frac{7}{25}$ | D. | -$\frac{7}{25}$ |
4.已知数列{an}的前n项和Sn=2n-1,则数列{an2}的前10项和为( )
| A. | 410-1 | B. | (210-1)2 | C. | $\frac{1}{3}$(410-1) | D. | $\frac{1}{3}$(210-1) |
5.已知平面向量$\overrightarrow{a}$=(2sin2x,cos2x),$\overrightarrow{b}$=(-sin2x,2cos2x),f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$.要得到y=$\sqrt{3}$sin2x-cos2x的图象,只需将y=f(x)的图象( )
| A. | 向左平移$\frac{π}{6}$个单位长度 | B. | 向右平移$\frac{π}{6}$个单位长度 | ||
| C. | 向左平移$\frac{π}{3}$个单位长度 | D. | 向右平移在$\frac{π}{3}$个单位长度 |
 一个多面体的直观图及三视图如图所示(其中M、N分别是AF、BC的中点).
一个多面体的直观图及三视图如图所示(其中M、N分别是AF、BC的中点).