题目内容
5. 一个多面体的直观图及三视图如图所示(其中M、N分别是AF、BC的中点).
一个多面体的直观图及三视图如图所示(其中M、N分别是AF、BC的中点).(1)求证:MN∥平面CDEF;
(2)求多面体A-CDEF的体积;
(3)求平面ADE与平面NMF所成的锐二面角的余弦值.
分析 由三视图可知:平面ABCD⊥平面ABFE,AD⊥平面ABFE,四边形ABCD是边长为2的正方形,底面ABFE是边长为2的正方形,M,N分别为AF,BC的中点.
(1)取BF的中点P,连接MP,NP.又M,N分别为AF,BC的中点.利用三角形中位线定理、面面平行的判定定理可得:平面MNP∥平面CDEF,即可证明MN∥平面CDEF.
(2)作AQ⊥DE,垂足为Q,利用线面垂直的判定与性质定理可得:AQ⊥平面CDEF.利用VA-CDEF=$\frac{1}{3}×AQ×{S}_{CDEF}$即可得出.
(3)利用平面BCF⊥平面ABFE,可得MP⊥平面BCF,过点P作PG⊥NF,可得:NF⊥MG,于是∠MGF为M-NF-B的二面角的平面角,即为平面ADE与平面NMF所成的锐二面角.利用直角三角形的边角关系即可得出.
解答 解:由三视图可知:平面ABCD⊥平面ABFE,AD⊥平面ABFE,
四边形ABCD是边长为2的正方形,底面ABFE是边长为2的正方形,M,N分别为AF,BC的中点.
(1)证明:取BF的中点P,连接MP,NP.
又M,N分别为AF,BC的中点.
∴NP∥CF,MP∥AB,
又AB∥EF,
可得MP∥EF.
又MP∩NP=P,MP?平面CDEF,NP?平面CDEF.
∴平面MNP∥平面CDEF;
∴MN∥平面CDEF.
(2)解:作AQ⊥DE,垂足为Q,
∵AD⊥平面ABFE,∴AD⊥EF.
又FE⊥AE,AD∩AE,
∴FE⊥平面ADE,
∴FE⊥AQ,
∴AQ⊥平面CDEF.
∵S四边形CDEF=EF•DE=$2×2\sqrt{2}$=4$\sqrt{2}$.
$AQ=\frac{AD•AE}{DE}$=$\frac{2×2}{2\sqrt{2}}$=$\sqrt{2}$.
∴VA-CDEF=$\frac{1}{3}×AQ×{S}_{CDEF}$=$\frac{1}{3}×\sqrt{2}×4\sqrt{2}$=$\frac{8}{3}$.
(3)解:∵平面BCF⊥平面ABFE,平面BCF∩平面ABFE=BF,MP⊥BF,∴MP⊥平面BCF,
过点P作PG⊥NF,连接MG,则NF⊥MG,
∴∠MGF为M-NF-B的二面角的平面角,即为平面ADE与平面NMF所成的锐二面角.
∵tan∠MFB=$\frac{1}{2}$,
∴sin∠MFB=$\frac{1}{\sqrt{5}}$,
在Rt△FPG中,PG=PF•sin∠PFG=$\frac{1}{\sqrt{5}}$.
∴tan∠MGF=$\frac{MP}{PG}$=$\frac{1}{\frac{1}{\sqrt{5}}}$=$\sqrt{5}$.
∴cos∠MGF=$\frac{\sqrt{6}}{6}$.
点评 本题考查了线面面面平行与垂直的判定及其性质定理、二面角、四棱锥的体积计算公式,考查了推理能力与计算能力,属于中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | ∅ | B. | {x|x=1} | C. | {x|1≤x≤2} | D. | {x|-1<x≤2} |


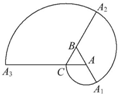 如图,△ABC是边长为1的正三角形,以A为圆心,AC为半径,沿逆时针方向画圆弧,交BA延长线于A1,记弧CA1的长为l1;以B为圆心,BA1为半径,沿逆时针方向画圆弧,交CB延长线于A2,记弧A1A2的长为l2;以C为圆心,CA2为半径,沿逆时针方向画圆弧,交AC延长线于A3,记弧A2A3的长为l3,则l1+l2+l3=4π.如此继续以A为圆心,AA3为半径,沿逆时针方向画圆弧,交AA1延长线于A4,记弧A3A4的长为l4,…,当弧长ln=8π时,n=12.
如图,△ABC是边长为1的正三角形,以A为圆心,AC为半径,沿逆时针方向画圆弧,交BA延长线于A1,记弧CA1的长为l1;以B为圆心,BA1为半径,沿逆时针方向画圆弧,交CB延长线于A2,记弧A1A2的长为l2;以C为圆心,CA2为半径,沿逆时针方向画圆弧,交AC延长线于A3,记弧A2A3的长为l3,则l1+l2+l3=4π.如此继续以A为圆心,AA3为半径,沿逆时针方向画圆弧,交AA1延长线于A4,记弧A3A4的长为l4,…,当弧长ln=8π时,n=12.