题目内容

6．曲线y=$\sqrt{2}$cosx在x=$\frac{π}{4}$处的切线的倾斜角是135°或$\frac{3π}{4}$．

分析 求函数的导数，利用导数的几何意义进行求解即可．

解答 解：∵$y'=-\sqrt{2}sinx$，$y'{|_{x=\frac{π}{4}}}=-1$
∴斜率k=-1，
由tanα=-1，
∴α=135°或$\frac{3π}{4}$，
故在x=$\frac{π}{4}$处的切线的倾斜角是135°或$\frac{3π}{4}$，
故答案为：135°或$\frac{3π}{4}$

点评 本题主要考查导数的几何意义，要求熟练掌握掌握常见函数的导数公式，比较基础．

练习册系列答案
相关题目
16．如图1所示的茎叶图是青年歌手电视大奖赛中7位评委给参加最后决赛的两位选手甲、乙评定的成绩，程序框图（图2）用来编写程序统计每位选手的成绩（各评委所给有效分数的平均值），试根据下面条件回答下列问题：

（1）根据茎叶图，乙选手的成绩中，中位数和众数分别是多少？
（2）在程序框图中，用k表示评委人数，用a表示选手的最后成绩（各评委所给有效分数的平均值）．那么图中①②处应填什么？“S1=S-max-min”的含义是什么？
（3）根据程序框图，甲、乙的最后成绩分别是多少？
（4）从甲、乙的有效分数中各取一个分数分别记作为x，y，若甲、乙的最后成绩分别是a，b，求“|x-a|≤1且|y-b|≤1”的概率．
17．执行如图所示的程序框图，则输出的T值为（　　）
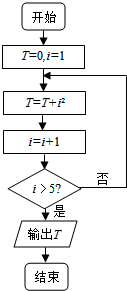
A．30B．54C．55D．91
14．过点A（1，2）且垂直于直线2x+y-5=0的直线方程为x-2y+3=0．
1．设数列{an}满足a1=0，${a_{n+1}}=\frac{1}{{b-{a_n}}}$，n∈N*．
（1）若b=2，求数列{an}的通项公式；
（2）令${c_n}=\frac{{{a_n}-p}}{{p{a_n}-1}}$（其中常数p＞0，且p≠1），若{cn}是等比数列，求实数b的取值范围．
11．已知函数$f（x）=|{1-\frac{1}{x}}|$，其中x＞0．
（1）当0＜a＜b且f（a）=f（b），求ab的取值范围；
（2）是否存在实数a、b（a＜b），使得函数y=f（x）的定义域和值域都是[a，b]，若存在，求出a、b的值，若不存在，说明理由；
（3）若存在a、b（a＜b），使得y=f（x）的定义域为[a，b]，值域为[ma，mb]（m≠0），求m的取值范围．
18．设函数y=$\frac{2{x}^{2}-x+n}{{x}^{2}+x+1}$（x∈R，x≠$\frac{n-2}{3}$，n∈N*）的最大值和最小值分别为an和bn，且cn=an+bn+anbn-15，Sn=|c1|+|c2|+|c3|+…+|cn|=$\left\{\begin{array}{l}{10n-2{n}^{2}，n≤3，n∈N+}\\{2{n}^{2}-10n+24，n≥4，n∈N+}\end{array}\right.$．
15．已知等比数列{an}满足a1=2，a2=4（a3-a4），数列{bn}满足bn=3-2log2an．
（Ⅰ）求数列{an}和{bn}的通项公式；
（Ⅱ）令cn=$\frac{a_n}{b_n}$，求数列{cn}的前n项和Tn；
（Ⅲ）若λ＞0，求对所有的正整数n都有2λ2-kλ+2＞a2nbn成立的k的范围．
16．已知集合A={x|x2-5x-6≥0}，B={x|-2≤x＜6}，则A∩B=（　　）
A．[-2，-1]B．[-1，6）C．[-1，3]D．[-2，6）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网