题目内容
【题目】在平面直角坐标系中，曲线C1的参数方程为 
（a＞b＞0，φ为参数），以Ο为极点，x轴的正半轴为极轴建立极坐标系，曲线C2是圆心在极轴上且经过极点的圆，已知曲线C1上的点M（2， 
）对应的参数φ= 
．θ= 
与曲线C2交于点D（ 
， ）．
（1）求曲线C1 ， C2的直角坐标方程；
（2）A（ρ1 ， θ），B（ρ2 ， θ+ 
）是曲线C1上的两点，求 
+ 
的值．
【答案】
（1）解：将曲线C1上的点M（2， 
）对应的参数φ= 
．
代入曲线C1的参数方程为 
（a＞b＞0，φ为参数），得：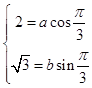 
解得： 
，
∴曲线C1的方程为： 
（φ为参数），即： 
．
设圆C2的半径R，则圆C2的方程为：ρ=2Rcosθ，将点D（ 
， 
）
代入得： =2R× 
，
∴R=1
∴圆C2的方程为：ρ=2cosθ即：（x﹣1）2+y2=1
（2）解：将A（ρ1，θ），Β（ρ2，θ+ 
）代入C1得： 
，
∴ 
+ 
=（ 
）+（ 
）= 
【解析】（1）将曲线C1上的点M（2， ）对应的参数φ= ．代入曲线C1的参数方程为 （a＞b＞0，φ为参数），即可解得：a，b．即可得出普通方程．设圆C2的半径R，则圆C2的方程为：ρ=2Rcosθ，将点D（ ， ）解得R可得圆C2的方程为：ρ=2cosθ，即可化为直角坐标方程．（2）将A（ρ1 ， θ），Β（ρ2 ， θ+ ）代入C1得： ， 
代入 + 即可得出．
练习册系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
