题目内容
【题目】已知函数f(x)是定义在R上的偶函数,且当x≤0时,f(x)=x2+2x.
(1)现已画出函数f(x)在y轴左侧的图象,如图所示,请补全函数f(x)的图象,并根据图象写出函数f(x)(x∈R)的递增区间; 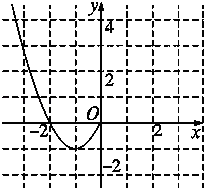
(2)写出函数f(x)(x∈R)的值域;
(3)写出函数f(x)(x∈R)的解析式.
【答案】
(1)解:根据偶函数的图象关于y轴对称,作出函数在R上的图象,
结合图象可得函数的增区间为(﹣1,0)、减区间为(1,+∞)
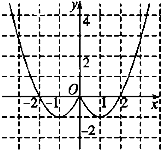
(2)解:结合函数的图象可得,当x=1,或 x=﹣1时,函数取得最小值为﹣1,
函数没有最大值,故函数的值域为[﹣1,+∞)
(3)解:当x>0时,﹣x<0,再根据x≤0时,f(x)=x2+2x,
可得f(﹣x)=(﹣x)2+2(﹣x)=x2﹣2x.
再根据函数f(x)为偶函数,可得f(x)=x2﹣2x.
综上可得,f(x)= ![]()
【解析】(1)根据偶函数的图象关于y轴对称,作出函数在R上的图象,结合图象可得函数的增区.(2)结合函数的图象可得函数的值域.(3)依据条件求得当x>0时,f(x)的解析式,再依据函数的奇偶性得到f(x)在R上的解析式.
【考点精析】通过灵活运用函数的值域和函数图象的作法,掌握求函数值域的方法和求函数最值的常用方法基本上是相同的.事实上,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值.因此求函数的最值与值域,其实质是相同的;图象的作法与平移:①据函数表达式,列表、描点、连光滑曲线;②利用熟知函数的图象的平移、翻转、伸缩变换;③利用反函数的图象与对称性描绘函数图象即可以解答此题.

练习册系列答案
相关题目