Question

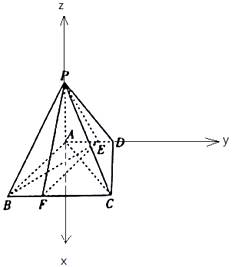
【题目】如图，四棱锥P﹣ABCD中，PA⊥底面ABCD，底面ABCD是直角梯形，∠ADC=90°，AD∥BC，AB⊥AC，AB=AC= ，点E在AD上，且AE=2ED．
（Ⅰ）已知点F在BC上，且CF=2FB，求证：平面PEF⊥平面PAC；
（Ⅱ）当二面角A﹣PB﹣E的余弦值为多少时，直线PC与平面PAB所成的角为45°？

Answer 1

【答案】（Ⅰ）证明：∵AB⊥AC，AB=AC，∴∠ACB=45°，

∵底面ABCD是直角梯形，∠ADC=90°，AD∥BC，

∴∠ACD=45°，即AD=CD，

∴ ，

∵AE=2ED，CF=2FB，∴ ，

∴四边形ABFE是平行四边形，则AB∥EF，

∴AC⊥EF，

∵PA⊥底面ABCD，∴PA⊥EF，

∵PA∩AC=A，

∴EF⊥平面PAC，∵EF平面PEF，

∴平面PEF⊥平面PAC．

（Ⅱ）解：∵PA⊥AC，AC⊥AB，

∴AC⊥平面PAB，

则∠APC为直线PC与平面PAB所成的角，

若PC与平面PAB所成夹角为45°，则 ，即 ，

取BC的中点为G，连接AG，则AG⊥BC，以A为坐标原点建立如图所示的空间直角坐标系A﹣xyz，

则B（1，﹣1，0），C（1，1，0）， ， ，

∴ ， ，

设平面PBE的法向量 ，则 即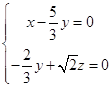

令y=3，则x=5， ，∴ ，

∵ 是平面PAB的一个法向量，

∴ ，

即当二面角A﹣PB﹣E的余弦值为 时，直线PC与平面PAB所成的角为45°．

【解析】（Ⅰ）推导出∠ACB=45°，从而∠ACD=45°，进而四边形ABFE是平行四边形，推导出AC⊥EF，PA⊥EF，从而EF⊥平面PAC，由此能证明平面PEF⊥平面PAC．（Ⅱ）由PA⊥AC，AC⊥AB，知AC⊥平面PAB，则∠APC为直线PC与平面PAB所成的角，取BC的中点为G，连接AG，则AG⊥BC，以A为坐标原点，建立空间直角坐标系A﹣xyz，利用向量法能求出直线PC与平面PAB所成的角．
【考点精析】解答此题的关键在于理解平面与平面垂直的判定的相关知识，掌握一个平面过另一个平面的垂线，则这两个平面垂直．