题目内容
【题目】某个实心零部件的形状是如图所示的几何体，其下部是底面均是正方形，侧面是全等的等腰梯形的四棱台A1B1C1D1﹣ABCD，其上是一个底面与四棱台的上底面重合，侧面是全等的矩形的四棱柱ABCD﹣A2B2C2D2 ． 
（1）证明：直线B1D1⊥平面ACC2A2；
（2）现需要对该零部件表面进行防腐处理，已知AB=10，A1B1=20，AA2=30，AA1=13（单位：厘米），每平方厘米的加工处理费为0.20元，需加工处理费多少元？
【答案】
（1）解：∵四棱柱ABCD﹣A2B2C2D2的侧面是全等的矩形，
∴AA2⊥AB，AA2⊥AD，又AB∩AD=A，
∴AA2⊥平面ABCD．连接BD，
∵BD平面ABCD，
∴AA2⊥BD，又底面ABCD是正方形，
∴AC⊥BD，根据棱台的定义可知，BD与B1D1共面，
又平面ABCD∥平面A1B1C1D1，且平面BB1D1D∩平面ABCD=BD，平面BB1D1D∩平面A1B1C1D1=B1D1，
∴B1D1∥BD，于是由AA2⊥BD，AC⊥BD，B1D1∥BD，可得AA2⊥B1D1，AC⊥B1D1，又AA2∩AC=A，
∴B1D1⊥平面ACC2A2
（2）解：∵四棱柱ABCD﹣A2B2C2D2的底面是正方形，侧面是全等的矩形，
∴S1=S四棱柱下底面+S四棱柱侧面
= 
+4ABAA2
=102+4×10×30
=1300（cm2）
又∵四棱台A1B1C1D1﹣ABCD上下底面均是正方形，侧面是全等的等腰梯形，
∴S2=S四棱柱下底面+S四棱台侧面
= 
+4× 
（AB+A1B1）h等腰梯形的高
=202+4× （10+20）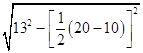 
=1120（cm2），
于是该实心零部件的表面积S=S1+S2=1300+1120=2420（cm2），
故所需加工处理费0.2S=0.2×2420=484元．
【解析】（1）依题意易证AC⊥B1D1 ， AA2⊥B1D1 ， 由线面垂直的判定定理可证直线B1D1⊥平面ACC2A2；（2）需计算上面四棱柱ABCD﹣A2B2C2D2的表面积（除去下底面的面积）S1 ， 四棱台A1B1C1D1﹣ABCD的表面积（除去下底面的面积）S2即可．
【考点精析】认真审题，首先需要了解直线与平面垂直的判定(一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直；注意点：a)定理中的“两条相交直线”这一条件不可忽视；b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想)．
