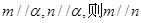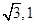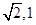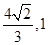题目内容
如图,三棱锥P ABC中,已知PA⊥平面ABC,△ABC是边长为2的正三角形,D,E分别为PB,PC中点

(1)若PA=2,求直线AE与PB所成角的余弦值;
(2)若PA ,求证:平面ADE⊥平面PBC
,求证:平面ADE⊥平面PBC

(1)若PA=2,求直线AE与PB所成角的余弦值;
(2)若PA
 ,求证:平面ADE⊥平面PBC
,求证:平面ADE⊥平面PBC(1)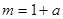 ,
, ;(2)
;(2)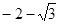
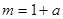 ,
, ;(2)
;(2)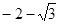
试题分析:(1)首先建立空间直角坐标系,给出相关点的坐标,利用空间向量求解;(2) 利用空间向量求解平面的法向量,然后根据法向量互相垂直可证明
试题解析:(1)如图,取AC的中点F,连接BF,则BF⊥AC 以A为坐标原点,过A且与FB平行的直线为x轴,AC为y轴,AP为z轴,建立空间直角坐标系

则A(0,0,0),B(,1,0), C(0,2,0),P(0,0,2),E(0,1,1),
从而=(,1, 2), =(0,1,1)
设直线AE与PB所成角为θ,
则cosθ=||=
即直线AE与PB所成角的余弦值为 5分
(2)如上图,则
A(0,0,0),B(,1,0), C(0,2,0),P(0,0,),E(0,1,
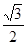 ),
),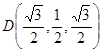
设平面PBC的法向量为
 ,则
,则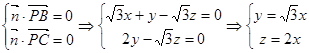
令
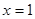 ,则
,则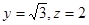 ,所以
,所以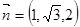
同理可求平面ADE的法向量
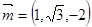
所以
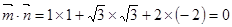 ,即
,即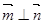
于是平面ADE⊥平面PBC

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
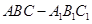 中, D是 AC的中点。
中, D是 AC的中点。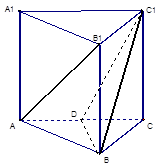
 //平面
//平面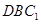
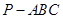 中,
中,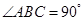 ,
,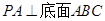

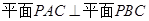 ;
;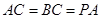 ,
,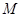 是
是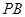 的中点,求
的中点,求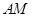 与平面
与平面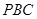 所成角的正切值
所成角的正切值 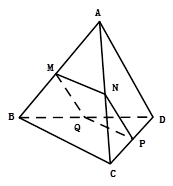
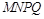 为平行四边形;
为平行四边形;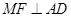 .
. 中,
中, ,
, ,
, .
. ;
;
 的正切值.
的正切值. 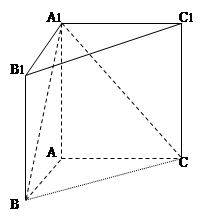
 ,下列说法正确的有: ___________.
,下列说法正确的有: ___________.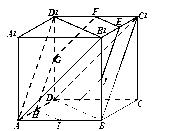
 点在线段
点在线段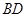 上运动,棱锥
上运动,棱锥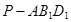 体积不变;
体积不变;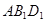 所成角不变;
所成角不变;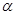 截此正方体,如果截面是三角形,则必为锐角三角形;
截此正方体,如果截面是三角形,则必为锐角三角形;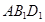 与平面
与平面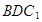 间平行移动时此六边形周长先增大,后减小。
间平行移动时此六边形周长先增大,后减小。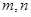 为两条不同的直线,
为两条不同的直线,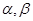 为两个不同的平面,给出下列4个命题:
为两个不同的平面,给出下列4个命题: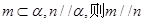 ②若
②若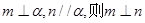
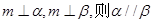 ④若
④若