Question

【题目】为了实现绿色发展，避免浪费能源，耨市政府计划对居民用电采用阶梯收费的方法.为此，相关部门在该市随机调查了20户居民六月份的用电量（单位：）和家庭收入（单位：万元），以了解这个城市家庭用电量的情况．

用电量数据如下：18,63,72,82,93,98,106,110,118,130,134,139,147,163,180,194,212,237,260,324．

对应的家庭收入数据如下：0.21，0.24，0.35,0.40,0.52,0.60,0.58,0.65,0.65,0.63,0.68,0.80,0.83，0.93,0.97,0.96,1.1,1.2,1.5,1.8.

（1）根据国家发改委的指示精神，该市计划实施3阶阶梯电价，使75%的用户在第一档，电价为0.56元/；的用户在第二档，电价为0.61元/；的用户在第三档，电价为0.86元/；试求出居民用电费用与用电量间的函数关系式；

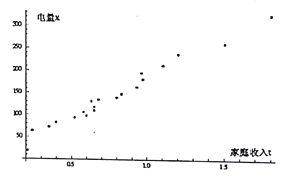
（2）以家庭收入为横坐标，电量为纵坐标作出散点图（如图），求关于的回归直线方程（回归直线方程的系数四舍五入保留整数）；

（3）小明家的月收入7000元，按上述关系，估计小明家月支出电费多少元？

参考数据：，，，，．

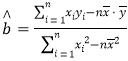参考公式：一组相关数据的回归直线方程的斜率和截距的最小二乘法估计分别为．，，其中为样本均值．

Answer 1

【答案】（1）；（2）；（3）72.8.

【解析】分析：（1）因为，

所以从用电量数据中得到第一档的临界值为第15个样本，即180，

第二档的临界值为第19个样本，即260．由此，可求居民用电费用与用电量间的函数关系式；

（2）计算可得，，代入公式可求关于的回归直线方程

（3）把代入回归直线方程求出，再把代入（1）函数解析式即可.

，所以，小明家月支出电费72.8元．

详解：（1）因为，

所以从用电量数据中得到第一档的临界值为第15个样本，即180，

第二档的临界值为第19个样本，即260．因此，

所以，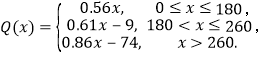

（2）由于，

，

，

所以，

从而回归直线方程为．

（3）当时，，

，所以，小明家月支出电费72.8元．