题目内容
若函数f(x)=(1-m)x2-2mx-5是偶函数,则f(x)在R上( )
| A.先减后增 | B.先增后减 | C.单调递增 | D.单调递减 |
f(x)=(1-m)x2-2mx-5是偶函数,
∴f(-x)=f(x)对任意的x都成立
即(1-m)x2-2mx-5=(1-m)x2+2mx-5对任意的x都成立
∴m=0
∴f(x)=x2-5在(-∞,0]单调递减,(0,+∞)单调递增
故选:A
∴f(-x)=f(x)对任意的x都成立
即(1-m)x2-2mx-5=(1-m)x2+2mx-5对任意的x都成立
∴m=0
∴f(x)=x2-5在(-∞,0]单调递减,(0,+∞)单调递增
故选:A

练习册系列答案
相关题目
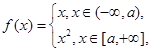 若
若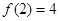 ,则
,则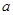 的取值范围为_____________.
的取值范围为_____________.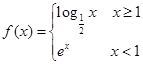 的值域为( )
的值域为( )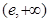
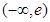
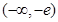
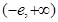
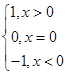 g(x)=
g(x)=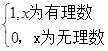 则f(g(π))的值为( ).
则f(g(π))的值为( ).