题目内容
【题目】设函数![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)若![]() ,证明
,证明![]() 恒成立.
恒成立.
【答案】(1)当![]() 时,
时,![]() 在区间
在区间![]() 上单调递增;当
上单调递增;当![]() 时,
时,![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增;(2)证明见详解.
上单调递增;(2)证明见详解.
【解析】
(1)求导,对参数进行分类讨论,进而求得函数的单调区间;
(2)将恒成立问题,转化两个函数最值之间的问题,进而求解.
(1)由题意得![]() ,
,![]() .
.
①当![]() 时,
时,![]() ,故函数
,故函数![]() 在区间
在区间![]() 上单调递增;
上单调递增;
②当![]() 时,在区间
时,在区间![]() 上,
上,![]() ,在区间
,在区间![]() 上,
上,![]() ,
,
故函数![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增.
上单调递增.
(2)证明:
要证![]() ,只需证
,只需证![]() .
.
又![]() ,故只需证
,故只需证![]() 即可.
即可.
设![]() ,则
,则![]() ,
,
在区间![]() 上,
上,![]() ,在区间
,在区间![]() 上,
上,![]() ,
,
故函数![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增,
上单调递增,
所以![]() .
.
设![]() ,则
,则![]() ,
,
在区间![]() 上,
上,![]() ,在区间
,在区间![]() 上,
上,![]() ,
,
故函数![]() 在区间
在区间![]() 上单调递增,在区间
上单调递增,在区间![]() 上单调递减,
上单调递减,
所以![]() .
.
又![]() ,所以
,所以![]() .
.
又因为![]() ,所以
,所以![]() ,
,
所以![]() ,
,
故在![]() 上,
上,![]() ,
,
综上,![]() 恒成立.
恒成立.

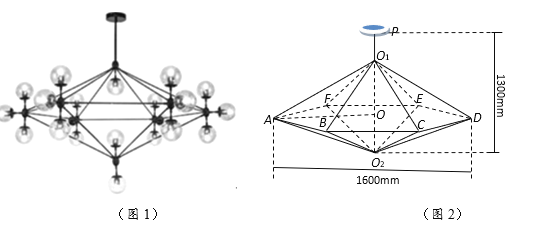
【题目】如图,在直角梯形![]() 中,
中,![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,以
,以![]() 为折痕把
为折痕把![]() 折起,当几何体
折起,当几何体![]() 的的体积最大时,则下列命题中正确的个数是( )
的的体积最大时,则下列命题中正确的个数是( )

①![]()
②![]() ∥平面
∥平面![]()
③![]() 与平面
与平面![]() 所成的角等于
所成的角等于![]() 与平面
与平面![]() 所成的角
所成的角
④![]() 与
与![]() 所成的角等于
所成的角等于![]() 与
与![]() 所成的角
所成的角
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【题目】《厉害了,我的国》是2018年在我国各影院上映的一部非常火的电影纪录片,该部影片主要讲述了我国近几年的发展现状和成就,影片通过讲述中国故事,刻画中国面貌,弘扬了中国精神,引起了国民的高度关注,上映仅半个月影片票房就突破了3亿元,刷新了我国纪录片的票房纪录,某市一电影院为了解该影院观看《厉害了,我的国》的观众的年龄构成情况,随机抽取了40名观众数据统计如表:
年龄/岁 | [10,20) | [20,30) | [30,40) | [40,50) | [50,60) | [60,70) | [70,80) |
人数 | 6 | 8 | 12 | 6 | 4 | 2 | 2 |
(1)求所调查的40名观众年龄的平均数和中位数;
(2)该电影院决定采用抽奖方式来提升观影人数,将《厉害了,我的国》的电影票票价提高20元/张,并允许购买电影票的观众抽奖3次,中奖1次、2次、3次分别奖现金20元、30元、60元,设观众每次中奖的概率均为![]() ,则观众在3次抽奖中所获得的奖金总额的数学期望是多少元(结果保留整数)?
,则观众在3次抽奖中所获得的奖金总额的数学期望是多少元(结果保留整数)?
【题目】某人经营淡水池塘养草鱼,根据过去![]() 期的养殖档案,该池塘的养殖重量
期的养殖档案,该池塘的养殖重量![]() (百斤)都在
(百斤)都在![]() 百斤以上,其中不足
百斤以上,其中不足![]() 百斤的
百斤的![]() 期,不低于
期,不低于![]() 百斤且不超过
百斤且不超过![]() 百斤的有
百斤的有![]() 期,超过
期,超过![]() 百斤的有
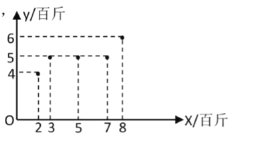
百斤的有![]() 期.根据统计,该池塘的草鱼重量的增加量
期.根据统计,该池塘的草鱼重量的增加量![]() (百斤)与使用某种饵料的质量
(百斤)与使用某种饵料的质量![]() (百斤)之间的关系如图所示.
(百斤)之间的关系如图所示.
鱼的重量(单位:百斤) |
|
|
|
冲水机运行台数 | 1 | 2 | 3 |
(1)根据数据可知![]() 与
与![]() 具有线性相关关系,请建立
具有线性相关关系,请建立![]() 关于
关于![]() 的回归方程
的回归方程![]() ;如果此人设想使用某种饵料
;如果此人设想使用某种饵料![]() 百斤时,草鱼重量的增加量须多于
百斤时,草鱼重量的增加量须多于![]() 百斤,请根据回归方程计算,确定此方案是否可行?并说明理由.
百斤,请根据回归方程计算,确定此方案是否可行?并说明理由.
(2)养鱼的池塘对水质含氧与新鲜度要求较高,故养殖户需设置若干台增氧冲水机,每期养殖使用的冲水机运行台数与鱼塘的鱼重量有关,并有如下关系:
若某台增氧冲水机运行,则该台冲水机每期盈利![]() 千元;若某台冲水机未运行,则该台冲水机每期亏损
千元;若某台冲水机未运行,则该台冲水机每期亏损![]() 千元.以频率 作为概率,养殖户欲使每期冲水机总利润的均值达到最大,应安装几台增氧冲水机?
千元.以频率 作为概率,养殖户欲使每期冲水机总利润的均值达到最大,应安装几台增氧冲水机?
附:对于一组数据![]() ,其回归方程
,其回归方程![]() 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为: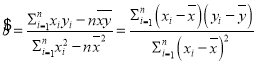 ,
,![]() .
.