题目内容
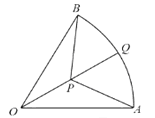
【题目】如图，三个校区分别位于扇形OAB的三个顶点上，点Q是弧AB的中点，现欲在线段OQ上找一处开挖工作坑P（不与点O，Q重合），为小区铺设三条地下电缆管线PO，PA，PB，已知OA＝2千米，∠AOB＝
，记∠APQ＝θrad，地下电缆管线的总长度为y千米．
（1）将y表示成θ的函数，并写出θ的范围；
（2）请确定工作坑P的位置，使地下电缆管线的总长度最小．
【答案】（1）
（2）P与O的距离为
时，地下电缆管线的总长度最小
【解析】
（1）首先根据Q为弧AB的中点，得到知PA＝PB，∠AOP＝∠BOP＝
，利用正弦定理得到
，根据OA＝2，得到PA＝
，OP＝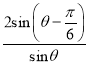
，从而得到y＝PA+PB+OP＝2PA+OP＝
＝
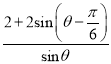，根据题意确定出；
（2）对函数求导，令导数等于零，求得
，确定出函数的单调区间，从而求得函数的最值.
（1）因为Q为弧AB的中点，由对称性，知PA＝PB，∠AOP＝∠BOP＝，
又∠APO＝
，∠OAP＝
，
由正弦定理，得：，又OA＝2，
所以，PA＝，OP＝，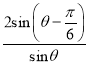
所以，y＝PA+PB+OP＝2PA+OP＝＝，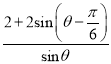
∠APQ＞∠AOP，所以，
，∠OAQ＝∠OQA＝
，
所以，；
（2）令
，
，得：，
在
上递减，在
上递增
所以，当，即OP＝时，有唯一的极小值，
即是最小值：
＝2
，
答：当工作坑P与O的距离为时，地下电缆管线的总长度最小．
【题目】某工厂为提高生产效率，开展技术创新活动，提出了完成某项生产任务的两种新的生产方式．为比较两种生产方式的效率，选取40名工人，将他们随机分成两组，每组20人，第一组工人用第一种生产方式，第二组工人用第二种生产方式．根据工人完成生产任务的工作时间（单位：min）绘制了如下茎叶图：
（1）根据茎叶图判断哪种生产方式的效率更高？并说明理由；
（2）求40名工人完成生产任务所需时间的中位数
，并将完成生产任务所需时间超过和不超过的工人数填入下面的列联表：
超过 | 不超过 | |
第一种生产方式 | ||
第二种生产方式 |
（3）根据（2）中的列联表，能否有99%的把握认为两种生产方式的效率有差异？
附：
，
|
|
|
|
|
|
|
|
