题目内容
已知向量a= ,b=
,b= ,设函数
,设函数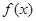 =a
=a b.
b.
(Ⅰ)求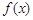 的单调递增区间;
的单调递增区间;
(Ⅱ)若将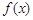 的图象向左平移
的图象向左平移 个单位,得到函数
个单位,得到函数 的图象,求函数
的图象,求函数 在区间
在区间 上的最大值和最小值.
上的最大值和最小值.
(Ⅰ)f(x)的递增区间是[- +kπ,
+kπ, +kπ]( k∈Z);(II)最大值为
+kπ]( k∈Z);(II)最大值为 +1,最小值为0.
+1,最小值为0.
解析试题分析:(Ⅰ)将f(x)=a•b=2sin2x+2sinxcosx降次化一,化为 的形式,然后利用正弦函数的单调区间,即可求得其单调递增区间.(II)将
的形式,然后利用正弦函数的单调区间,即可求得其单调递增区间.(II)将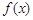 的图象向左平移
的图象向左平移 个单位,则将
个单位,则将 换成
换成 得到函数
得到函数 的解析式g(x)=
的解析式g(x)= sin[2(x+
sin[2(x+ )-
)- ]+1=
]+1= sin(2x+
sin(2x+ )+1.由
)+1.由 ≤x≤
≤x≤ 得
得 ≤2x+
≤2x+ ≤
≤ ,结合正弦函数的图象可得0≤g(x)≤
,结合正弦函数的图象可得0≤g(x)≤ +1,从而得g(x)的最大值和最小值.
+1,从而得g(x)的最大值和最小值.
试题解析:(Ⅰ)f(x)=a•b=2sin2x+2sinxcosx
= +sin2x
+sin2x
= sin(2x-
sin(2x- )+1, 3分
)+1, 3分
由- +2kπ≤2x-
+2kπ≤2x- ≤
≤ +2kπ,k∈Z,得-
+2kπ,k∈Z,得- +kπ≤x≤
+kπ≤x≤ +kπ,k∈Z,
+kπ,k∈Z,
∴f(x)的递增区间是[- +kπ,
+kπ, +kπ](k∈Z). 6分
+kπ](k∈Z). 6分
(II)由题意g(x)= sin[2(x+
sin[2(x+ )-
)- ]+1=
]+1= sin(2x+
sin(2x+ )+1, 9分
)+1, 9分
由 ≤x≤
≤x≤ 得
得 ≤2x+
≤2x+ ≤
≤ ,
,
∴ 0≤g(x)≤ +1,即 g(x)的最大值为
+1,即 g(x)的最大值为 +1,g(x)的最小值为0. 12分
+1,g(x)的最小值为0. 12分
考点:1、向量及三角恒等变换;2、三角函数的单调区间及范围.

练习册系列答案
相关题目
 . 的部分图象如图所示,其中点
. 的部分图象如图所示,其中点 是图象的一个最高点.
是图象的一个最高点.
 的解析式;
的解析式; 且
且 ,求
,求 .
. sin ωx-sin2
sin ωx-sin2 +
+ (ω>0)的最小正周期为π.
(ω>0)的最小正周期为π. 时,求函数f(x)的取值范围.
时,求函数f(x)的取值范围. 的周期为
的周期为 .
.
 ,求它的振幅、初相;
,求它的振幅、初相;  的图像;
的图像; 的不同取值,讨论函数
的不同取值,讨论函数 的零点个数.
的零点个数. .
.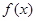 的最小正周期和图像的对称轴方程;
的最小正周期和图像的对称轴方程; 上的值域.
上的值域. ,钝角
,钝角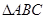 (角
(角 对边为
对边为 )的角
)的角 满足
满足 .
. 的单调递增区间;
的单调递增区间; ,求
,求 .
.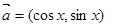 ,
, ,函数
,函数 。
。 的值域和函数的单调递增区间;
的值域和函数的单调递增区间;  ,且
,且 时,求
时,求 的值.
的值. .
. 在角
在角 的终边上,求
的终边上,求 的值;(Ⅱ)若
的值;(Ⅱ)若 ,求
,求 的值域.
的值域. (
( )的最小正周期为
)的最小正周期为 .求函数
.求函数 的单调增区间;
的单调增区间; 中,角
中,角 对边分别是
对边分别是 ,且满足
,且满足 .若
.若 ,
, .求角
.求角 的大小和边b的长.
的大小和边b的长.