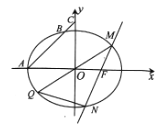
题目内容
【题目】如图所示,正方形AA1D1D与矩形ABCD所在平面互相垂直,AB=2AD=2,点E为AB的中点. 
(1)求证:BD1∥平面A1DE;
(2)求直线A1E与平面AD1E所成角.
【答案】
(1)证明:连接AD1交A1D于点F,连EF.
∵四边形AA1D1D是正方形,
∴F是AD1的中点,
又∵E为AB的中点,
∴EF∥BD1,
又∵EF平面A1DE,BD1平面A1DE.
∴BD1∥平面A1DE.
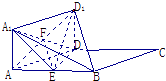
(2)解:∵四边形ABCD是矩形,
∴AE⊥AD.
又∵平面AA1D1D⊥平面ABCD,平面AA1D1D∩平面ABCD=AD,AE平面ABCD,
∴AE⊥平面AA1D1D,又A1D平面AA1D1D,
∴AE⊥A1D.
∵四边形ADD1A1是正方形,
∴AD1⊥A1D,
又∵AE平面AD1E,AD1平面AD1E,AE∩AD1=A,
∴A1D⊥平面AD1E,
∴∠A1EF是直线A1E与平面AD1E所成角.
∵AA1=AE=1,
∴ ![]()
∵正方形AA1D1D的边长为1,
∴ ![]()
∴ ![]() ,
,
∴ ![]() .
.
即直线A1E与平面AD1E所成角为 ![]() .
.
【解析】(1)连接AD1交A1D于点F,连EF,利用中位线定理可得BD1∥EF,故BD1∥平面A1DE;(2)证明A1D⊥平面AD1E,故而∠A1EF为直线A1E与平面AD1E所成角,于是sin∠A1EF= ![]() .
.
【考点精析】根据题目的已知条件,利用直线与平面平行的判定和空间角的异面直线所成的角的相关知识可以得到问题的答案,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则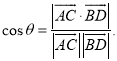 .
.

 提分百分百检测卷系列答案
提分百分百检测卷系列答案【题目】已知函数f(x)=Asin(ωx+φ)+B(A>0,ω>0)的一系列对应值如表:
x | ﹣ |
|
|
|
|
|
|
y | ﹣1 | 1 | 3 | 1 | ﹣1 | 1 | 3 |
(1)根据表格提供的数据求函数f(x)的一个解析式;
(2)根据(1)的结果:
( i)当x∈[0, ![]() ]时,方程f(3x)=m恰有两个不同的解,求实数m的取值范围;
]时,方程f(3x)=m恰有两个不同的解,求实数m的取值范围;
( ii)若α,β是锐角三角形的两个内角,试比较f(sinα)与f(cosβ)的大小.
【题目】某媒体对“男女延迟退休”这一公众关注的问题进行了民意调查,如表是在某单位得到的数据(人数):
(1)能否有90%以上的把握认为对这一问题的看法与性别有关?
赞同 | 反对 | 合计 | |
男 | 5 | 6 | 11 |
女 | 11 | 3 | 14 |
合计 | 16 | 9 | 25 |
(2)从赞同“男女延迟退休”16人中选出3人进行陈 述发言,求事件“男士和女士各至少有1人发言”的概率;
(3)若以这25人的样本数据来估计整个地区的总体数据,现从该地区(人数很多)任选5人,记赞同“男女延迟退休”的人数为X,求X的数学期望.
附:
p(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
K2= ![]() .
.