题目内容
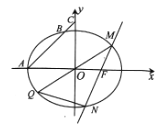
【题目】【2017重庆二诊】已知椭圆![]() :
: ![]() 的左顶点为
的左顶点为![]() ,右焦点为
,右焦点为![]() ,过点
,过点![]() 且斜率为1的直线交椭圆
且斜率为1的直线交椭圆![]() 于另一点
于另一点![]() ,交
,交![]() 轴于点
轴于点![]() ,
, ![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 作直线
作直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,连接
两点,连接![]() (
(![]() 为坐标原点)并延长交椭圆
为坐标原点)并延长交椭圆![]() 于点
于点![]() ,求
,求![]() 面积的最大值及取最大值时直线
面积的最大值及取最大值时直线![]() 的方程.
的方程.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ) ![]() 面积的最大值为3,此时直线
面积的最大值为3,此时直线![]() 的方程为
的方程为![]()
【解析】(Ⅰ)由已知,易知求得点![]() ,
, ![]() 的坐标,由
的坐标,由![]() ,利用向量的坐标表示可求得点
,利用向量的坐标表示可求得点![]() 坐标,联立右焦点坐标及椭圆中
坐标,联立右焦点坐标及椭圆中![]() 关系式,代入椭圆方程进行运算即可;(Ⅱ)由椭圆对称性得,
关系式,代入椭圆方程进行运算即可;(Ⅱ)由椭圆对称性得, ![]() ,由题意,联立直线与椭圆的方程,求得
,由题意,联立直线与椭圆的方程,求得![]() 的底边长
的底边长![]() ,再由点到直线距离公式求得
,再由点到直线距离公式求得![]() 的高,从而建立所求三角形面积的函数,通过求面积函数的最大值,从而问题可得解.
的高,从而建立所求三角形面积的函数,通过求面积函数的最大值,从而问题可得解.
试题解析:(Ⅰ)由题知![]() ,故
,故![]() ,代入椭圆
,代入椭圆![]() 的方程得
的方程得![]() ,又
,又![]() ,
,
故![]() ,椭圆
,椭圆![]() ;
;
(Ⅱ)由题知,直线![]() 不与
不与![]() 轴重合,故可设
轴重合,故可设![]() ,由
,由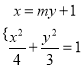 得
得![]() ,
,
设![]() ,则
,则![]() ,由
,由![]() 与
与![]() 关于原点对称知,
关于原点对称知,
![]()
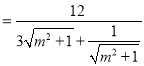 ,
,
![]() ,
, ![]() ,即
,即![]() ,当且仅当
,当且仅当![]() 时等号成立,
时等号成立,
![]() 面积的最大值为3,此时直线
面积的最大值为3,此时直线![]() 的方程为
的方程为![]()

 阅读快车系列答案
阅读快车系列答案【题目】某市举办校园足球赛,组委会为了做好服务工作,招募了12名男志愿者和10名女志愿者,调查发现男女志愿者中分别有8人和4人喜欢看足球比赛,其余不喜欢
(1)根据以上数据完成以下2×2列联表:
喜欢看足球比赛 | 不喜欢看足球比赛 | 总计 | |
男 | |||
女 | |||
总计 |
(2)根据列联表的独立性检验,能否在犯错误的概率不超过0.10的前提下认为性别与喜欢看足球比赛有关?
(3)从女志愿者中抽取2人参加某场足球比赛服务工作,若其中喜欢看足球比赛的人数为ξ,求ξ的分布列和数学期望.
附:参考公式:K2= ![]() ,其中n=a+b+c+d
,其中n=a+b+c+d
参考数据:
P(K2≥k0) | 0.4 | 0.25 | 0.10 | 0.010 |
k0 | 0.708 | 1.323 | 2.706 | 6.635 |
【题目】【2017湖南长沙二模】某种产品的质量以其质量指标值衡量,并依据质量指标值划分等极如下表:
质量指标值 |
|
|
|
等级 | 三等品 | 二等品 | 一等品 |
从某企业生产的这种产品中抽取200件,检测后得到如下的频率分布直方图:

(1)根据以上抽样调查数据 ,能否认为该企业生产的这种产品符合“一、二等品至少要占全部产品90%”的规定?
(2)在样本中,按产品等极用分层抽样的方法抽取8件,再从这8件产品中随机抽取4件,求抽取的4件产品中,一、二、三等品都有的概率;
(3)该企业为提高产品质量,开展了“质量提升月”活动,活动后再抽样检测,产品质量指标值![]() 近似满足
近似满足![]() ,则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少?
,则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少?