题目内容
【题目】（本小题满分16分）
在平面直角坐标系xOy中，椭圆C：
（a＞b＞0）的上顶点到焦点的距离为2，离心率为
．
（1）求a，b的值．
（2）设P是椭圆C长轴上的一个动点，过点P作斜率为k的直线l交椭圆C于A、B两点．
（ⅰ）若k＝1，求△OAB面积的最大值；
（ⅱ）若PA2＋PB2的值与点P的位置无关，求k的值．
【答案】（1）
＋y2＝1．（2）（ⅰ）m＝±
时，S△OAB取得最大值1．（ⅱ）±
.
【解析】
试题分析：（1）由椭圆几何条件知上顶点到焦点的距离为半长轴长，即a＝2，又e
，所以c＝
，故b＝1．（2）（ⅰ）求△OAB面积的最大值，关键建立其函数关系式，这要用到点到直线距离公式来求高，利用两点间距离公式来求底边边长：设点P（m，0）（－2≤m≤2），直线l的方程为y＝x－m．则可求得∣AB|＝
，高为
，从而S△OAB＝
×|m|，利用基本不等式求最值（ⅱ）由题意先表示出PA2＋PB2，再按m整理，最后根据与点P的位置无关得到对应项系数为零，从而解出k的值．
试题解析：（1）由题设可知a＝2，e，所以c＝，故b＝1．
因此，a＝2，b＝1． 2分
（2）由（1）可得，椭圆C的方程为＋y2＝1．
设点P（m，0）（－2≤m≤2），点A（x1，y1），点B（x2，y2）．
(ⅰ)若k＝1，则直线l的方程为y＝x－m．
联立直线l与椭圆C的方程，即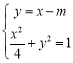
．将y消去，化简得
－2mx＋m2－1＝0．从而有x1＋x2＝
， x1· x2＝
，
而y1＝x1－m，y2＝x2－m，
因此，∣AB|＝
点O到直线l的距离d＝，
所以，S△OAB＝×|AB|×d＝×|m|，
因此，S2△OAB＝
( 5－m2)×m2≤
＝1．
6分
又－2≤m≤2，即m2∈[0，4]．
所以，当5－m2＝m2，即m2＝
， m＝±时，S△OAB取得最大值1．
8分
(ⅱ)设直线l的方程为y＝k(x－m).
将直线l与椭圆C的方程联立，即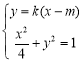
．
将y消去，化简得(1＋4k2)x2－8mk2x＋4(k2m2－1)＝0，解此方程，可得，
x1＋x2＝
，x1·x2＝
． 10分
所以，
PA2＋PB2＝(x1－m)2＋y12＋(x2－m)2＋y22＝
(x12＋x22)－2m(x1＋x2)＋2m2＋2
＝
（*）. 14分
因为PA2＋PB2的值与点P的位置无关，即（*）式取值与m无关，
所以有－8k4－6k2＋2＝0，解得k＝±．
所以，k的值为±. 16分
