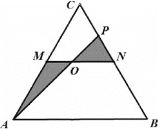
题目内容
【题目】过抛物线![]() (其中
(其中![]() )的焦点
)的焦点![]() 的直线交抛物线于
的直线交抛物线于![]() 两点,且
两点,且![]() 两点的纵坐标之积为
两点的纵坐标之积为![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)当![]() 时,求
时,求![]() 的值;
的值;
(3)对于![]() 轴上给定的点
轴上给定的点![]() (其中
(其中![]() ),若过点
),若过点![]() 和
和![]() 两点的直线交抛物线
两点的直线交抛物线![]() 的准线
的准线![]() 点,求证:直线
点,求证:直线![]() 与
与![]() 轴交于一定点.
轴交于一定点.
【答案】(1)![]() ; (2)1; (3)见解析.
; (2)1; (3)见解析.
【解析】
(1)设直线AB的方程,联立抛物线方程,运用韦达定理,可得p=4,即得抛物线方程;(2)推理证明![]() =
=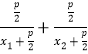 ,整理即可得到所求值;(3)设A(
,整理即可得到所求值;(3)设A(![]() ,y1),B(
,y1),B(![]() ,y2),P(﹣2,s),运用三点共线的条件:斜率相等,可得s,设AP交x轴上的点为(t,0),运用韦达定理,化简整理可得所求定点.
,y2),P(﹣2,s),运用三点共线的条件:斜率相等,可得s,设AP交x轴上的点为(t,0),运用韦达定理,化简整理可得所求定点.
(1)过抛物线![]() (其中
(其中![]() )的焦点
)的焦点![]() 的直线
的直线
为![]() ,代入抛物线方程,可得
,代入抛物线方程,可得![]() ,
,
可设![]() ,
,
即有![]() ,解得
,解得![]() ,
,
可得抛物线的方程为![]() ;
;
(2)由直线![]() 过抛物线的焦点
过抛物线的焦点![]() ,
,
由(1)可得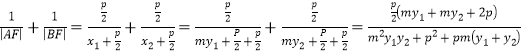 ,将
,将![]() 代入可得
代入可得![]() ;
;
(3)证明:设![]() ,
,![]() ,
,![]() ,
,
由![]() 三点共线可得
三点共线可得
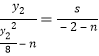 ,可得
,可得![]() ,①
,①
设![]() 交
交![]() 轴上的点为
轴上的点为![]() ,即有
,即有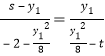 ,
,
代入①,结合![]() ,可得
,可得![]() ,
,
即有![]() ,
,
可得![]() .即有直线
.即有直线![]() 与
与![]() 轴交于一定点
轴交于一定点![]() .
.

【题目】(1)某校夏令营有3名男同学A、B、C和3名女同学X、Y、Z,其年级情况如下表:
一年级 | 二年级 | 三年级 | |
男同学 | A | B | C |
女同学 | X | Y | Z |
现从这6名同学中随机选出2人参加知识竞赛(每人被选到的可能性相同).
①用表中字母列举出所有可能的结果;
②设M为事件“选出的2人来自不同年级且恰有1名男同学和1名女同学”,求事件M发生的概率.
(2)节日前夕,小李在家门前的树上挂了两串彩灯.这两串彩灯的第一次闪亮相互独立,且都在通电后的4秒内任一时刻等可能发生,然后每串彩灯以4秒为间隔闪亮.那么这两串彩灯同时通电后,它们第一次闪亮的时刻相差不超过2秒的概率是多少?
【题目】设某地区乡居民人民币储蓄存款(年底余额)如下表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
时间代号x | 1 | 2 | 3 | 4 | 5 | 6 |
储蓄存款y(千亿元) | 3.5 | 5 | 6 | 7 | 8 | 9.5 |
(1)求关于x的回归方程![]() ,并预测该地区2019年的人民币储蓄存款(用最简分数作答).
,并预测该地区2019年的人民币储蓄存款(用最简分数作答).
(2)在含有一个解释变量的线性模型中,![]() 恰好等于相关系数r的平方,当
恰好等于相关系数r的平方,当![]() 时,认为线性冋归模型是有效的,请计算
时,认为线性冋归模型是有效的,请计算![]() 并且评价模型的拟合效果(计算结果精确到0.001).
并且评价模型的拟合效果(计算结果精确到0.001).
附:
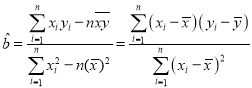 ,
,
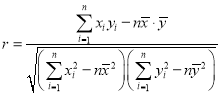
![]()