题目内容
【题目】一个创业青年租用一块边长为4百米的等边![]() 田地
田地![]() 如图
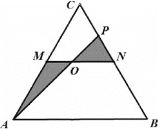
如图![]() 养蜂、产蜜与售蜜,田地内拟修建笔直小路MN,AP,其中M,N分别为AC,BC的中点,点P在CN上,
养蜂、产蜜与售蜜,田地内拟修建笔直小路MN,AP,其中M,N分别为AC,BC的中点,点P在CN上,![]() 规划在小路MN与AP的交点O(O与M、N不重合
规划在小路MN与AP的交点O(O与M、N不重合![]() 处设立售蜜点,图中阴影部分为蜂巢区,空白部分为蜂源植物生长区,A,N为出入口
处设立售蜜点,图中阴影部分为蜂巢区,空白部分为蜂源植物生长区,A,N为出入口![]() 小路的宽度不计
小路的宽度不计![]() 为节约资金,小路MO段与OP段建便道,供蜂源植物培育之用,费用忽略不计
为节约资金,小路MO段与OP段建便道,供蜂源植物培育之用,费用忽略不计![]() 为车辆安全出入,小路AO段的建造费用为每百米5万元,小路ON段的建造费用为每百米4万元.
为车辆安全出入,小路AO段的建造费用为每百米5万元,小路ON段的建造费用为每百米4万元.
(Ⅰ)若拟修的小路AO段长为![]() 百米,求小路ON段的建造费用;
百米,求小路ON段的建造费用;
(Ⅱ)设![]() , 求
, 求![]() 的值,使得小路AO段与ON段的建造总费用最小.
的值,使得小路AO段与ON段的建造总费用最小.
【答案】(Ⅰ)4万元;(Ⅱ)![]() ,小路AO段与ON段的建造总费用最小为
,小路AO段与ON段的建造总费用最小为![]() 万元.
万元.
【解析】
(Ⅰ)在![]() 中用余弦定理计算
中用余弦定理计算![]() 的长度,故可得
的长度,故可得![]() 的长度后即得
的长度后即得![]() 段的建筑费用.
段的建筑费用.
(Ⅱ)在![]() 中用正弦定理计算
中用正弦定理计算![]() 的长度后得到
的长度后得到![]() ,令
,令![]() ,将其变形为
,将其变形为![]() ,利用辅助角公式可得
,利用辅助角公式可得![]() ,从而得到
,从而得到![]() ,验证等号成立后可得何时取最小值.
,验证等号成立后可得何时取最小值.
(Ⅰ)在![]() 中,
中,![]() ,
,
![]() 即
即![]() ,
,
故![]() 或
或![]() (舎去),故
(舎去),故![]() ,
,
所以![]() 段的建筑费用为
段的建筑费用为![]() 万元.
万元.
(Ⅱ)由正弦定理得:在![]() 中,
中,![]() ,
,
故![]() ,
,
![]()
设小路![]() 和
和![]() 段的建造总费用为
段的建造总费用为![]() ,
,
则![]() ,
,
令![]() ,且
,且![]() ,
,![]() ,
,
![]() 即
即![]() .
.
由![]() ,得
,得![]() ,故
,故![]() ,即
,即![]() 或
或![]() (舍去).
(舍去).
当![]() 时,
时,![]() ,故
,故![]() ,其中
,其中![]() ,
,
故由![]() ,符合题意.
,符合题意.
答:![]() ,小路AO段与ON段的建造总费用最小为
,小路AO段与ON段的建造总费用最小为![]() 万元.
万元.

练习册系列答案
相关题目