��Ŀ����
����Ŀ����1��ijУ����Ӫ��3����ͬѧA��B��C��3��ŮͬѧX��Y��Z�����꼶������±���
һ�꼶 | ���꼶 | ���꼶 | |
��ͬѧ | A | B | C |
Ůͬѧ | X | Y | Z |
�ִ���6��ͬѧ�����ѡ��2�˲μ�֪ʶ����(ÿ�˱�ѡ���Ŀ�������ͬ)��
���ñ�����ĸ�оٳ����п��ܵĽ����
����MΪ�¼���ѡ����2�����Բ�ͬ�꼶��ǡ��1����ͬѧ��1��Ůͬѧ�������¼�M�����ĸ��ʣ�
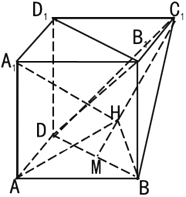
��2������ǰϦ��С���ڼ���ǰ�����Ϲ��������ʵƣ��������ʵƵĵ�һ��������������Ҷ���ͨ����4������һʱ�̵ȿ��ܷ�����Ȼ��ÿ���ʵ���4��Ϊ�����������ô�������ʵ�ͬʱͨ������ǵ�һ��������ʱ��������2��ĸ����Ƕ��٣�
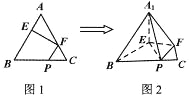
���𰸡���1�������������![]() ��2��
��2��![]()
��������
��1�����ñ�����ĸһһ�оٳ����п��ܵĽ������15����
�����оٷ�����¼�![]() �����Ľ����6�������Ϲŵ���͵��������ɴ�����¼�
�����Ľ����6�������Ϲŵ���͵��������ɴ�����¼�![]() �����ĸ��ʣ�
�����ĸ��ʣ�
��2�����ϼ��θ��͵����������һ���ʵ�����ʱ��Ϊ![]() ���ڶ����ʵ�����ʱ��Ϊ
���ڶ����ʵ�����ʱ��Ϊ![]() ���ò���ʽ��ʾ������������ͼ�������֮��������ʣ�
���ò���ʽ��ʾ������������ͼ�������֮��������ʣ�
�⣺��1���ٴ�6��ͬѧ�����ѡ��2�˲μ�֪ʶ���������п��ܽ��Ϊ![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ����15�֣�
����15�֣�
��ѡ����2�����Բ�ͬ�꼶��ǡ��1����ͬѧ��1��Ůͬѧ�����п��ܽ��Ϊ![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ����6�֣�
����6�֣�
��ˣ��¼�M�����ĸ���![]() ��
��
��2�����һ���ʵ�����ʱ��Ϊ![]() ���ڶ����ʵ�����ʱ��Ϊ
���ڶ����ʵ�����ʱ��Ϊ![]() ����
����![]() ��
��
Ҫʹ�����ʵ�����ʱ��������2�룬��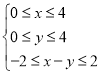 ��
��
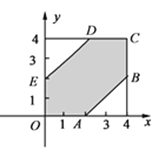
��ͼ������ʽ��![]() ����ʾ��ͼ�����Ϊ16��
����ʾ��ͼ�����Ϊ16��
����ʽ��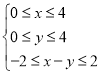 ����ʾ�������ε����Ϊ
����ʾ�������ε����Ϊ![]() ��
��
�ɼ��θ��͵Ĺ�ʽ�ɵ�![]() ��
��

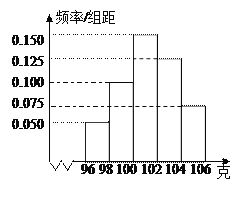
����Ŀ�������ҹ����õķ��ٷ�չ����������ˮƽ�õ��ܴ���ߣ������Ѿ�����ǧǧ����ļ�ͥ.�ֵij����ڹ�������ʱ�����ڽγ�����![]() ������ѡ��Ϊ���о�ij�������ֳ����ܻ�ӭ�Լ�����һ���ڵ���ʻ��̣�ij�������۾�����������ͳ�ƣ�
������ѡ��Ϊ���о�ij�������ֳ����ܻ�ӭ�Լ�����һ���ڵ���ʻ��̣�ij�������۾�����������ͳ�ƣ�
�����˽γ������� | ������ | |
|
|
|
|
|
|
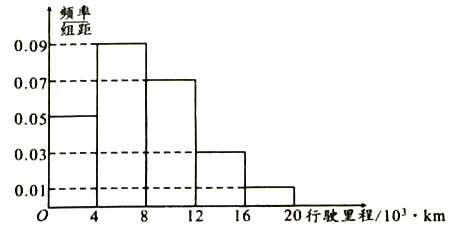
��1�����ݱ����Ƿ���![]() �İ�����Ϊ�����빺������������йأ�
�İ�����Ϊ�����빺������������йأ�
��2��ͼ��������![]() ��������һ����������ʻ��̣�����
��������һ����������ʻ��̣�����![]() ��������һ��������ƽ����ʻ��̣�ͬһ���е������ø���������е�ֵ����������
��������һ��������ƽ����ʻ��̣�ͬһ���е������ø���������е�ֵ����������
��3���÷ֲ�����ķ�����![]() �����ϳ����г�ȡ
�����ϳ����г�ȡ![]() �ˣ��ٴ���
�ˣ��ٴ���![]() ���������ȡ
���������ȡ![]() ��������ѱ���ȯ������
��������ѱ���ȯ������![]() ����������
����������![]() ���γ��ĸ��ʡ�
���γ��ĸ��ʡ�
����![]() ��
��![]()
|
|
|
|
|
|
|
|
|
|