题目内容
【题目】已知直线l的极坐标方程为ρsin（θ+ 
）= 
．
（1）在极坐标系下写出θ=0和θ= 
时该直线上的两点的极坐标，并画出该直线；
（2）已知Q是曲线ρ=1上的任意一点，求点Q到直线l的最短距离及此时Q的极坐标．
【答案】
（1）解：直线l经过A（2，0）， 
两点，
在极坐标系下，直线如图所示：
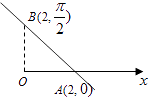
（2）解：曲线ρ=1化为直角坐标方程得x2+y2=1，该曲线为单位圆，
将直线l的极坐标方程 
化为直角坐标方程得x+y﹣2=0
要求圆上任意一点到直线l的最短距离，只要求圆心O（0，0）到直线l的距离即可．
由点到直线的距离公式得： 
，
所以点Q到直线l的最短距离为 
，
此时，点Q的极坐标为 
．
【解析】（1）将θ=0和θ= 
分别代入直线l的极坐标方程，求出ρ，从而得出两点的极坐标，画出直线；（2）分别求出直线l和曲线ρ=1的直角坐标方程，要求圆上任意一点到直线l的最短距离，只要求圆心O（0，0）到直线l的距离即可．
练习册系列答案
相关题目
