题目内容
【题目】已知0＜β＜α＜ 
，tanα=4 
，cos（α﹣β）= 
．
（1）求sin2α的值；
（2）求β的大小．
【答案】
（1）解：因为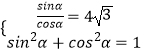 
，且 
，所以，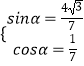 
，
所以， 
（2）解：因为 
，所以 
，又因为 
，所以， ，
所以cosβ=cos[α﹣（α﹣β）]= 
．
因为 
，所以 
【解析】（1）由条件利用同角三角函数的基本关系求得sinα、cosα的值，可得sin2α的值．（2）由条件利用同角三角函数的基本关系求得sin（α﹣β）的值，可得cosβ=cos[α﹣（α﹣β）]的值，结合β的范围求得β的值．
【考点精析】解答此题的关键在于理解同角三角函数基本关系的运用的相关知识，掌握同角三角函数的基本关系：
；
;（3） 倒数关系：
．
【题目】学校从参加高一年级期中考试的学生中抽出50名学生，并统计了他们的数学成绩（成绩均为整数且满分为150分），数学成绩分组及各组频数如下：
[60，75），2；[75，90），3；[90，105），14；[105，120），15；[120，135），12；[135，150]，4．
（1）在给出的样本频率分布表中，求A，B，C，D的值；
（2）估计成绩在120分以上（含120分）学生的比例；
（3）为了帮助成绩差的学生提高数学成绩，学校决定成立“二帮一”小组，即从成绩在[135，150]的学生中选两位同学，共同帮助成绩在[60，75）中的某一位同学．已知甲同学的成绩为62分，乙同学的成绩为140分，求甲、乙两同学恰好被安排在同一小组的概率．
样本频率分布表：
分组 | 频数 | 频率 |
[60，75） | 2 | 0.04 |
[75，90） | 3 | 0.06 |
[90，105） | 14 | 0.28 |
[105，120） | 15 | 0.30 |
[120，135） | A | B |
[135，150] | 4 | 0.08 |
合计 | C | D |
