题目内容
【题目】已知函数![]() ,
, ![]() .
.
(1)若关于![]() 的不等式
的不等式![]() 在
在![]() 上恒成立,求
上恒成立,求![]() 的取值范围;
的取值范围;
(2)设函数![]() ,若
,若![]() 在
在![]() 上存在极值,求
上存在极值,求![]() 的取值范围,并判断极值的正负.
的取值范围,并判断极值的正负.
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】【试题分析】(1)先分离参数,再构造函数运用导数求函数的最值;(2)借助导数与函数的单调性之间的关系,运用分类整合思想进行分析求解:
(1)由![]() ,得
,得![]() ,即
,即![]() 在
在![]() 上恒成立.
上恒成立.
设函数![]() ,
, ![]() .则
.则![]() .
.
设![]() .则
.则![]() .易知当
.易知当![]() 时,
时, ![]() .
.
∴![]() 在
在![]() 上单调递增,且
上单调递增,且![]() .即
.即![]() 对
对![]() 恒成立.
恒成立.
∴![]() 在
在![]() 上单调递增,∴当
上单调递增,∴当![]() 时,
时, ![]() .
.
∴![]() ,即
,即![]() 的取值范围是
的取值范围是![]() .
.
(2)![]() ,
, ![]() ,∴
,∴![]() .
.
设![]() ,则
,则![]() .由
.由![]() ,得
,得![]() .
.
当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() . ∴
. ∴![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.且
上单调递减.且![]() ,
, ![]() ,
, ![]() .显然
.显然![]() .
.
结合函数图像可知,若![]() 在
在![]() 上存在极值,则
上存在极值,则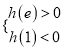 或
或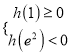 .
.
(ⅰ)当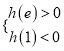 ,即
,即![]() 时,
时,
则必定![]() ,使得
,使得![]() ,且
,且![]() .
.
当![]() 变化时,
变化时, ![]() ,
, ![]() ,
, ![]() 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 极小值 |
| 极大值 |
|
∴当![]() 时,
时, ![]() 在
在![]() 上的极值为
上的极值为![]() ,且
,且![]() .
.
∵![]() .
.
设![]() ,其中
,其中![]() ,
, ![]() .
.
∵![]() ,∴
,∴![]() 在
在![]() 上单调递增,
上单调递增, ![]() ,当且仅当
,当且仅当![]() 时取等号.
时取等号.
∵![]() ,∴
,∴![]() .∴当
.∴当![]() 时,
时, ![]() 在
在![]() 上的极值
上的极值![]() .
.
(ⅱ)当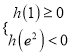 ,即
,即![]() 时,则必定
时,则必定![]() ,使得
,使得![]() .
.
易知![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.此时,
上单调递减.此时, ![]() 在
在![]() 上的极大值是
上的极大值是![]() ,且
,且![]() .
.
∴当![]() 时,
时, ![]() 在
在![]() 上极值为正数.综上所述:当
上极值为正数.综上所述:当![]() 时,
时, ![]() 在
在![]() 上存在极值.且极值都为正数.
上存在极值.且极值都为正数.
注:也可由![]() ,得
,得![]() .令
.令![]() 后再研究
后再研究![]() 在
在![]() 上的极值问题.
上的极值问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目