题目内容
【题目】已知函数f(x)=ex(其中e为自然对数的底数),g(x)=![]() x+m(m,n∈R).
x+m(m,n∈R).
(1)若T(x)=f(x)g(x),m=1﹣![]() ,求T(x)在[0,1]上的最大值;
,求T(x)在[0,1]上的最大值;
(2)若m=﹣![]() ,n∈N*,求使f(x)的图象恒在g(x)图象上方的最大正整数n.[注意:7<e2<
,n∈N*,求使f(x)的图象恒在g(x)图象上方的最大正整数n.[注意:7<e2<![]() ].
].
【答案】(1)当![]() 时最大值为
时最大值为![]() ;当
;当![]() 时最大值为
时最大值为![]() (2)14
(2)14
【解析】试题分析:
(1)首先求得函数的解析式,然后利用导函数研究函数的最值可得当![]() 时最大值为
时最大值为![]() ;当
;当![]() 时最大值为
时最大值为![]() ;
;
(2)将问题转化为![]() 恒成立,讨论可得最大正整数n为14.
恒成立,讨论可得最大正整数n为14.
试题解析:
解:(1)T(x)=f(x)g(x)
=ex(![]() x+m)=ex(
x+m)=ex(![]() x+1﹣
x+1﹣![]() );
);
故T′(x)=ex(![]() x+1);
x+1);
则当n≥﹣2时,T′(x)≥0;
故T(x)在[0,1]上的最大值为T(1)=e;
当n<﹣2时,x∈[0,﹣![]() )时,T′(x)>0;x∈(﹣
)时,T′(x)>0;x∈(﹣![]() ,1]时,T′(x)<0;
,1]时,T′(x)<0;
T(x)在[0,1]上的最大值为T(﹣![]() )=﹣
)=﹣![]()
![]() ;
;
(2)由题意,f(x)=ex,g(x)=![]() x﹣
x﹣![]() ;
;
故f(x)的图象恒在g(x)图象上方可化为
F(x)=f(x)﹣g(x)=ex﹣![]() x+
x+![]() >0恒成立;F′(x)=ex﹣
>0恒成立;F′(x)=ex﹣![]() ;
;
故F(x)在(﹣∞,ln![]() )上是减函数,在(ln
)上是减函数,在(ln![]() ,+∞)上是增函数;
,+∞)上是增函数;
故可化为F(ln![]() )>0;即
)>0;即![]() (1﹣ln
(1﹣ln![]() )+
)+![]() >0;
>0;
令G(n)=![]() (1﹣ln
(1﹣ln![]() )+
)+![]() ;故G′(n)=﹣
;故G′(n)=﹣![]() (ln
(ln![]() +1)<0;
+1)<0;
故G(n)=![]() (1﹣ln
(1﹣ln![]() )+
)+![]() 是[1,+∞)上的减函数,
是[1,+∞)上的减函数,
而G(2e2)=﹣e2+![]() >0;G(14)=7(1﹣ln7)+
>0;G(14)=7(1﹣ln7)+![]() >0;
>0;
G(15)=7.5(1﹣ln7.5)+![]() <0;故最大正整数n为14.
<0;故最大正整数n为14.

 阅读快车系列答案
阅读快车系列答案【题目】某校为了探索一种新的教学模式,进行了一项课题实验,甲班为实验班,乙班为对比班,甲乙两班的人数均为50人,一年后对两班进行测试,测试成绩的分组区间为[80,90)、[90,100)、[100,110)、[110,120)、[120,130),由此得到两个班测试成绩的频率分布直方图: 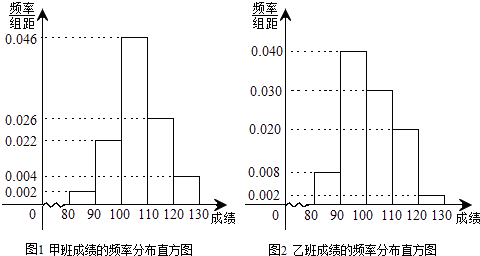
(1)完成下面2×2列联表,你能有97.5%的把握认为“这两个班在这次测试中成绩的差异与实施课题实验有关”吗?并说明理由;
成绩小于100分 | 成绩不小于100分 | 合计 | |
甲班 | a= | b= | 50 |
乙班 | c=24 | d=26 | 50 |
合计 | e= | f= | 100 |
(2)现从乙班50人中任意抽取3人,记ξ表示抽到测试成绩在[100,120)的人数,求ξ的分布列和数学期望Eξ.
附:K2= ![]() ,其中n=a+b+c+d
,其中n=a+b+c+d
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.204 | 6.635 | 7.879 | 10.828 |