题目内容

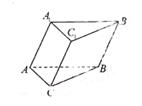
长方体ABCD-A1B1C1D1中，对角线AC1与AB、AD、AA1所成角分别为α、β、θ，则cos2α+cos2β+cos2θ=______．
以AC1为斜边构成直角三角形：△AC1D，AC1B，AC1A1，
由长方体的对角线长定理可得
cos2α+cos2β+cos2θ=
AB2
AC12
+
AD2
AC12
+
AA12
AC12
=
A
C21
A
C21
=1．
故答案为：1．
练习册系列答案
相关题目
如图，在三棱柱ABC-A1B1C1中，∠ACB=900,∠ACC1=600,∠BCC1=450,侧棱CC1的长为1，则该三棱柱的高等于（）
A．B．C．D．
圆台的上下底面半径和高的比为1：4：4，母线长为10，则其表面积为______．
圆柱侧面展开图是一个边长为2的正方形，则其体积为______．
如图，在三棱锥P-ABC中，∠APB=∠BPC=∠APC=90°，M在△ABC内，∠MPA=60°，∠MPB=45°，则∠MPC的度数为（　　）
A．30°B．45°C．60°D．75°
圆x2+（y+1）2=3绕直线y=kx-1旋转一周所得的几何体的体积为（　　）
A．36πB．12πC．4
3
π		D．4π
已知六棱锥P-ABCDEF的底面是正六边形，PA⊥平面ABC．则下列结论不正确的是（　　）
A．CD∥平面PAFB．DF⊥平面PAFC．CF∥平面PABD．CF⊥平面PAD
棱长为a的正方体ABCD-A1B1C1D1的8个顶点都在球O的表面上，E、F分别是棱AA1、DD1的中点，则直线EF被球O截得的线段长为______．
一几何体的直观图如右图，下列给出的四个俯视图中正确的是（   ）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网