题目内容
8.函数f(x)=$\sqrt{4-{x}^{2}}$+$\frac{1}{ln(x+1)}$的定义域为(-1,0)∪(0,2].分析 根据二次根式以及对数函数的性质得到不等式组,解出即可.
解答 解:由题意得:
$\left\{\begin{array}{l}{4{-x}^{2}≥0}\\{x+1>0}\\{x+1≠1}\end{array}\right.$,解得:-1<x≤2且x≠0,
故答案为:(-1,0)∪(0,2].
点评 本题考查了二次根式的性质,对数函数的性质,是一道基础题.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
18.执行如图所示的程序框图,如果输入的N=5,那么输出的S等于( )
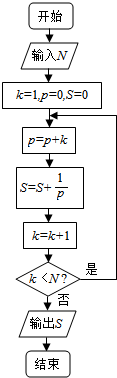

| A. | $\frac{7}{4}$ | B. | $\frac{8}{5}$ | C. | $\frac{16}{9}$ | D. | $\frac{20}{11}$ |
16.某几何体的三视图如图,则该几何体的体积为( )
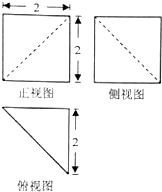

| A. | $\frac{8}{3}$ | B. | $\frac{8\sqrt{2}}{3}$ | C. | $\frac{4}{3}$ | D. | $\frac{4\sqrt{2}}{3}$ |
3.设a=0.82.1,b=21.1,c=log23,则( )
| A. | b<c<a | B. | c<a<b | C. | a<b<c | D. | a<c<b |
13.在△ABC中,AB=2,BC=2.5,∠ABC=120°,若使△ABC绕直线BC旋转一周,则所形成的几何体的体积是( )
| A. | $\frac{9π}{2}$ | B. | $\frac{7π}{2}$ | C. | $\frac{5π}{2}$ | D. | $\frac{3π}{2}$ |
20.某几何体的三视图如图所示,则该几何体的体积为( )
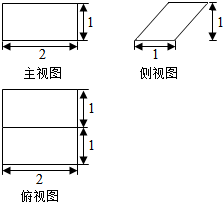

| A. | 1 | B. | 2 | C. | 2$\sqrt{2}$ | D. | $\frac{2}{3}$ |
20.在△ABC中,角A为钝角,AB=1,AC=3,AD为BC边上的高,已知$\overrightarrow{AD}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$,则x的取值范围为( )
| A. | ($\frac{3}{4}$,$\frac{9}{10}$) | B. | ($\frac{1}{2}$,$\frac{9}{10}$) | C. | ($\frac{3}{5}$,$\frac{3}{4}$) | D. | ($\frac{1}{2}$,$\frac{3}{4}$) |
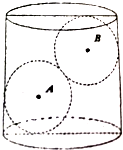 如图,在水平放置的直径与高相等的圆柱内,放入两个半径相等的小球(球A和球B),圆柱的底面直径为2+$\sqrt{2}$,向圆柱内注满水,水面刚好淹没小球B
如图,在水平放置的直径与高相等的圆柱内,放入两个半径相等的小球(球A和球B),圆柱的底面直径为2+$\sqrt{2}$,向圆柱内注满水,水面刚好淹没小球B