Question

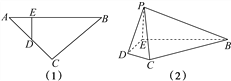
【题目】如图(1)，等腰直角三角形ABC的底边AB＝4，点D在线段AC上，DE⊥AB于E，现将△ADE沿DE折起到△PDE的位置(如图(2))．

(1)求证：PB⊥DE；

(2)若PE⊥BE，PE＝1，求点B到平面PEC的距离．

Answer 1

【答案】（1）详见解析（2）

【解析】试题分析：（1）根据线面垂直的判定定理和性质定理进行证明，（2）由(1)知PE⊥平面BEDC，在△EDC中，由余弦定理得EC＝，S△PEC＝×PE×EC＝.利用等体积法VP－BEC＝VB－PEC进行求解即可得点B到平面PEC的距离．

试题解析：

(1)∵DE⊥AB，∴DE⊥PE，DE⊥EB.

又∵PE∩BE＝E，∴DE⊥平面PEB.∵PB平面PEB，∴PB⊥DE.

(2)由(1)知DE⊥PE，且PE⊥BE，DE∩BE＝E，∴PE⊥平面BEDC.

连接EC，∵PE＝1，

∴DE＝PE＝1，AD＝DC＝.

在△EDC中，∠EDC＝135°，由余弦定理得

EC2＝DE2＋DC2－2DE×DC×cos∠EDC＝1＋2－2×(－)＝5，

∴EC＝，∴S△PEC＝×PE×EC＝.

设点B到平面PEC的距离为h，则由VP－BEC＝VB－PEC得S△PEC·h＝S△BEC·PE，

∴h＝×3×2×1，∴h＝.